La continuità in topologia
Siano \(X\) e \(Y\) due spazi topologici. Una funzione \(f: X \to Y\) è detta continua se, per ogni insieme aperto \(V\) in \(Y\), la controimmagine \(f^{-1}(V)\) è un insieme aperto in \(X\).
In altre parole, una funzione continua in topologia "preserva" la struttura degli insiemi aperti quando mappa punti da un insieme all'altro.
La continuità in topologia riguarda il mantenimento della "coerenza" degli insiemi aperti tra uno spazio e l'altro.
Nota. La continuità in topologia è una generalizzazione del concetto di continuità in analisi matematica, che non si basa sulla distanza tra i punti. In analisi, la continuità è legata alla vicinanza dei punti; in topologia, invece, riguarda il modo in cui una funzione interagisce con la struttura degli insiemi aperti. In altre parole, la definizione topologica mi permette di stabilire se una funzione "rispetta" la struttura degli insiemi aperti, anche in situazioni in cui non posso parlare di vicinanza tra i punti.
Ad esempio, "allungo" o "deformo" una forma geometrica senza strapparla. Questa deformazione può essere rappresentata da una funzione continua.
La continuità mi assicura che la struttura originale (come gli insiemi aperti) rimane intatta dopo la trasformazione.
Un esempio pratico
Considero due insiemi spazi topologici $ X = \{a, b, c, d\} $ e $ Y = \{1, 2\} $
- Nello spazio \( X \) gli insiemi aperti sono: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
- Nello spazio \( Y \) gli insiemi aperti sono: \(\{\}, \{1\}, \{1, 2\}\).
Ho una funzione \( f: X \rightarrow Y \) che collega i due spazi topologici:
\( f(a) = 1 \), \( f(b) = 1 \), \( f(c) = 2 \), \( f(d) = 2 \)
Secondo la definizione di continuità topologica, questa funzione è continua oppure no?
Per avere una visione di insieme, rappresento la funzione $ f $ e i due spazi topologici, cerchiando gli insiemi aperti nei rispettivi spazi.
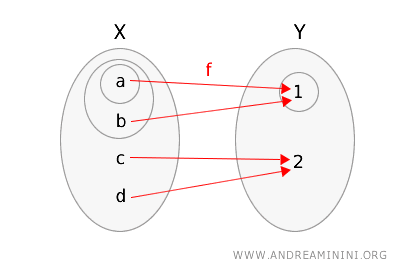
A questo punto verifico se la definizione di continuità topologica è soddisfatta.
- Prendo l'insieme aperto \(\{1\}\) in \( Y \), la sua controimmagine in \( X \) è \( f^{-1}(\{1\}) = \{a, b\} \). Questo insieme \(\{a, b\}\) è aperto in \( X \)
- Prendo l'insieme aperto \(\{1, 2\}\) in \( Y \), la sua controimmagine è \( f^{-1}(\{1, 2\}) = \{a, b, c, d\} \). Anche questo è un insieme aperto in \( X \).
Tralascio di verificare gli insiemi vuoti perché sono aperti in ogni topologia.
In conclusione, poiché ogni controimmagine di un insieme aperto in \( Y \) è aperta in \( X \), la funzione $ f $ è continua.
Esempio 2
Prendo in considerazione una funzione diversa \( g: X \rightarrow Y \) tra gli stessi spazi topologici dell'esempio precedente.
\( g(a) = 1 \), \( g(b) = 1 \), \( g(c) = 1 \), \( g(d) = 2 \)
Rappresento la funzione $ g $ e i due spazi topologici cerchiando gli insiemi aperti.
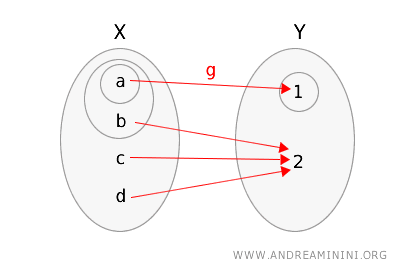
Infine, verifico se viene soddisfatta la definizione di continuità topologica.
- Prendo l'insieme aperto \(\{1\}\) in \( Y \), la sua controimmagine in \( X \) è \( g^{-1}(\{1\}) = \{a, b, c\} \). Questo insieme non è aperto in \( X \).
Poiché c'è almeno un insieme aperto in \( Y \) la cui controimmagine non è aperta in \( X \), posso affermare che la funzione \( g \) non è continua.
Esempio 3
In questo esempio prendo in considerazione una semplice funzione identità \( id: X \to X \) definita come \( id(x) = x \) per ogni \( x \in X \).
$$ x = f(x) $$
Intuitivamente, la funzione identità non "cambia" nulla. In termini topologici, questo significa che l'immagine dell'insieme aperto in \( X \) è ancora un insieme aperto in \( X \).
Quindi, la funzione identità \( f(x)=x \) è sempre continua, perché non c'è nessun cambiamento nello spazio topologico di \( X \) quando applico la funzione identità.
Esempio 4
Considero una funzione costante \( f: X \to Y \) è definita come \( f(x) = c \) per ogni \( x \in X \).
$$ f(x) = c $$
In altre parole, qualunque sia l'elemento \( x \) di \( X \) che scelgo, la funzione costante "ignora" \( x \) e restituisce sempre lo stesso valore \( c \).
La definizione di continuità in topologia richiede che, per ogni insieme aperto \( V \) in \( Y \), l'insieme preimmagine \( f^{-1}(V) \) sia aperto in \( X \).
A questo punto ci sono due possibilità:
- Se \( c \) appartiene a \( V \), cioè l'elemento fisso che ho scelto è dentro l'insieme aperto \( V \)), allora la preimmagine di \( V \) tramite \( f \) è tutto lo spazio \( X \) perché \( f(x) = c \) per tutti gli \( x \)). Siccome l'intero spazio \( X \) è un insieme aperto, allora \( f^{-1}(V) = X \) è aperto.
- Se \( c \) non appartiene a \( V \), cioè l'elemento fisso è fuori da \( V \)), allora la preimmagine di \( V \) tramite \( f \) è l'insieme vuoto (\( \emptyset \)). Anche l'insieme vuoto è aperto.
In entrambi i casi, la preimmagine \( f^{-1}(V) \) è un insieme aperto in \( X \).
Di conseguenza, la funzione costante \( f(x)=c \) è continua.
Nota. Questo esempio sottolinea che la continuità di una funzione in topologia non dipende solo dalla "formula" della funzione stessa, ma anche dalle strutture topologiche degli spazi su cui si sto lavorando. Nel caso della funzione costante, la sua preimmagine di qualsiasi insieme aperto in \( Y \) è sempre un insieme aperto in \( X \), quindi la funzione è continua.
Esempio 5
Considero di nuovo la funzione identità \( f : X \to Y \) ovvero $ f(x)=x $ ma tra due spazi topologici diversi, dove:
- \( X \) è lo spazio dei numeri reali \( \mathbb{R} \) con la topologia standard dove gli insiemi aperti sono intervalli del tipo \( (a,b) \), poiché ogni punto di un insieme aperto deve avere un intorno completamente contenuto all'interno dell'insieme stesso.
- \( Y \) è lo spazio dei numeri reali \( \mathbb{R} \) con la topologia del limite inferiore dove gli insiemi aperti sono intervalli del tipo \([a, b)\)).
Per capire se la funzione \( f \) è continua, devo verificare se la preimmagine di un insieme aperto in \( Y \) è un insieme aperto in \( X \).
Prendo un tipico insieme aperto nello spazio \( Y \), ad esempio \( [0, 1) \). Questo insieme è aperto nella topologia del limite inferiore.
La preimmagine di \( [0, 1) \) tramite \( f \) è semplicemente \( [0, 1) \), perché \( f \) è la funzione identità, quindi \( f^{-1}([0, 1)) = [0, 1) \).
Nella topologia standard, l'intervallo \( [0, 1) \) non è un insieme aperto.
Nota. Nella topologia standard un insieme è aperto se, per ogni punto, esiste un intervallo aperto attorno a quel punto contenuto nell'insieme. Nel caso di \( [0, 1) \), il punto \( 0 \) non ha un intervallo attorno a sé che sia interamente contenuto in \( [0, 1) \), perché qualsiasi intervallo attorno a \( 0 \) includerebbe numeri negativi, che non sono in \( [0, 1) \).
Pertanto, la funzione identità \( f : \mathbb{R} \to \mathbb{R} \), con \( \mathbb{R} \) che ha la topologia standard nel dominio e la topologia del limite inferiore nel codominio, non è continua.
Questo perché ci sono insiemi aperti in \( Y \) (come \( [0, 1) \)) la cui preimmagine non è aperta nella topologia standard.
Questo esempio dimostra che la continuità in topologia non dipende soltanto dalla funzione in sé, ma dalle topologie definite sul dominio e sul codominio.
Infatti, la funzione identità \( f(x) = x \) è la stessa del primo esempio ma in questo caso non è continua.
Il teorema delle basi nella continuità
Dati due spazi topologici \( X \) e \( Y \), una funzione \( f: X \to Y \) è continua se e solo se, per ogni insieme di base \( B_Y \) della topologia su \( Y \), la controimmagine \( f^{-1}(B_Y) \) è un insieme aperto in \( X \).
Questo teorema è molto utile nella pratica perché mi permette di semplificare la verifica della continuità di una funzione.
Invece di controllare la controimmagine di tutti gli insiemi aperti di \( Y \), mi basta verificare la controimmagine di un numero molto più ridotto di insiemi: quelli che formano una base per la topologia su \( Y \).
Questo riduce notevolmente il numero dei controlli,rendendo la verifica della continuità molto più rapida.
Dimostrazione. Ogni insieme aperto in \( Y \) può essere scritto come un'unione di insiemi della sua base \( B_Y \). Quindi, se la controimmagine di ciascun insieme della base \( B_Y \) è aperta in \( X \), posso dedurre che anche la controimmagine di tutti gli insiemi aperti di \( Y \) sarà aperta in \( X \), poiché questi insiemi aperti sono ottenuti dall'unione di insiemi di base. Questo implica che la condizione di continuità è soddisfatta e, di conseguenza, la funzione \( f: X \to Y \) è continua.
Esempio
Considero due spazi topologici \( X = \{a, b, c, d\} \) e \( Y = \{x, y, z\} \) con le seguenti topologie:
- La topologia su \( X \) è: \( \tau_X = \{\emptyset, \{a\}, \{a, b\}, \{a, b, c, d\} \} \).
- La topologia su \( Y \) ha come base \( B_Y = \{\{x\}, \{y\}, \{z\}\} \).
In questo caso la topologia completa su \( Y \) è l'unione di elementi della base. Quindi, posso costruire molti insiemi aperti che non sono direttamente elementi della base, ma sono unioni di questi ultimi.
Ad esempio, gli insiemi \( \{x, y\} \), \( \{x, z\} \), \( \{y, z\} \), e \( \{x, y, z\} \) non appartengono alla base $ B_Y $, ma sono comunque altri insiemi aperti dello spazio $ Y $ perché ottenuti dall'unione di elementi della base.
Una funzione \( f: X \to Y \) è definita come segue:
- \( f(a) = x \)
- \( f(b) = x \)
- \( f(c) = y \)
- \( f(d) = z \)
Per verificare se la funzione è continua, analizzo se le controimmagini degli insiemi di base \( B_Y = \{\{x\}, \{y\}, \{z\}\} \) della topologia su \( Y \) sono aperte nello spazio \( X \)
- \( f^{-1}(\{x\}) = \{a, b\} \) che è un insieme aperto in \( X \)
- \( f^{-1}(\{y\}) = \{c\} \) che non è un insieme aperto in \( X \) poiché non appartiene alla topologia \( \tau_X \). In altre parole $ \{c\} $ manca nella topologia su \( X \).
Poiché la controimmagine di \( \{y\} \) non è aperta in \( X \), posso affermare con certezza che la funzione \( f \) non è continua, dato che non soddisfa la condizione che la controimmagine di ogni insieme di base su \( Y \) sia aperta in \( X \).
Nota. Quando la controimmagine di un insieme di base in \( Y \) non è aperta in \( X \), non è necessario verificare ulteriori controimmagini. Una volta accertato che la controimmagine \( f^{-1}(\{y\}) = \{c\} \) non è aperta, il controllo dell'apertura della controimmagine di \( \{z\} \) diventa superfluo. È infatti sufficiente che anche una sola controimmagine di un insieme di base di \( Y \) non sia aperta in \( X \) per concludere che la funzione non è continua.
La continuità in una topologia grossolana e in una topologia fine
Se una funzione è continua rispetto alla topologia più grossolana, allora è continua anche rispetto alla topologia più fine.
Tuttavia, il contrario non è necessariamente vero: una funzione può essere continua rispetto alla topologia più fine ma non rispetto alla più grossolana.
Nota. Date due topologie sullo stesso insieme $ X $, una topologia è "più grossolana" dell'altra se ha meno insiemi aperti. Viceversa, è detta "più fine" dell'altra se ha più insiemi aperti.
Esempio
Considero l'insieme \( X = \{a, b\} \) con due topologie:
- Topologia più grossolana \( \tau_1 = \{\varnothing, \{a, b\}\} \) dove solo l'insieme vuoto e l'insieme completo \( \{a, b\} \) sono aperti.
- Topologia più fine \( \tau_2 = \{\varnothing, \{a\}, \{b\}, \{a, b\}\} \) dove anche il sottoinsieme \( \{a\} \) e il sottoinsieme \( \{b\} \) sono aperti oltre all'insieme completo.
Definisco ora una funzione \( f: X \to Y \), dove \( Y = \{1\} \), come segue:
$$ f(a) = 1 $$
$$ f(b) = 1 $$
Nella topologia più grossolana \( \tau_1 \), gli insiemi aperti sono \( \varnothing \) e \( \{a, b\} \).
Verifico la continuità della funzione \( f \):
- \( f^{-1}(\varnothing) = \varnothing \) è l'insieme vuoto che per definizione è aperto anche in \( \tau_1 \)
- \( f^{-1}(\{1\}) = \{a, b\} \) è aperto anche in \( \tau_1 \)
Poiché \( \{a, b\} \) è aperto in \( \tau_1 \), la funzione $ f $ è continua rispetto alla topologia grossolana \( \tau_1 \).
Pertanto, la funzione $ f $ deve essere continua anche rispetto alla topologia più fine \( \tau_2 \) perché le controimmagini sono le stesse.
Nella topologia più fine \( \tau_2 \), gli insiemi aperti sono \( \varnothing \), \( \{a\} \), \( \{b\} \), e \( \{a, b\} \).
- \( f^{-1}(\varnothing) = \varnothing \) è aperto anche in \( \tau_2 \)
- \( f^{-1}(\{1\}) = \{a, b\} \) è aperto anche in \( \tau_2 \)
Poiché \( \{a, b\} \) è aperto anche in \( \tau_2 \), la funzione \( f \) è continua anche rispetto alla topologia fine \( \tau_2 \).
In conclusione, la funzione \( f \) è continua sia rispetto alla topologia grossolana che alla topologia più fine, perché la topologia più fine ha più insiemi aperti, ma ogni insieme aperto della topologia grossolana è anche aperto in quella più fine.
Tuttavia, il contrario non è necessariamente vero. Una funzione può essere continua nella topologia più fine, ma non essere continua in una topologia più grossolana, perché quest'ultima ha meno insiemi aperti e quindi impone meno restrizioni sulla continuità.
Esempio 2
Considero di nuovo l'insieme \( X = \{a, b\} \) con le stesse topologie:
- Topologia più grossolana \( \tau_1 = \{\varnothing, \{a, b\}\} \)
- Topologia più fine \( \tau_2 = \{\varnothing, \{a\}, \{b\}, \{a, b\}\} \)
Definisco ora una funzione \(gf: X \to Y \), dove \( Y = \{1,2\} \), come segue:
$$ g(a) = 1 $$
$$ g(b) = 2 $$
La funzione $ g $ è continua rispetto alla topologia più fine $ \tau_2 $ perché tutte le controimmagini di $ Y $ sono aperte in $ \tau_2 $
- \( g^{-1}(\varnothing) = \varnothing \) è aperto in \( \tau_2 \)
- \( g^{-1}( \{1,2 \} ) = \{a,b\} \) è aperto in \( \tau_2 \)
- \( g^{-1}( \{1 \} ) = \{a\} \) è aperto anche in \( \tau_2 \)
- \( g^{-1}( \{2 \} ) = \{b\} \) è aperto anche in \( \tau_2 \)
In questo caso, però, la funzione $ g $ non è continua rispetto alla topologia grossolana $ \tau_1 $ perché alcune controimmagini di $ Y $ non sono aperte in $ \tau_1 $
- \( g^{-1}(\varnothing) = \varnothing \) è aperto in \( \tau_1 \)
- \( g^{-1}( \{1,2 \} ) = \{a,b\} \) è aperto in \( \tau_1 \)
- \( g^{-1}( \{1 \} ) = \{a\} \) non è aperto in \( \tau_1 \)
In conclusione, la funzione $ g $ è continua rispetto alla topologia fine $ \tau_2 $ ma non è continua rispetto alla topologia grossolana $ \tau_1 $.
La differenza tra connessione e continuità
La connessione e la continuità non sono la stessa cosa, anche se entrambe riguardano proprietà di coesione nello spazio topologico.
- La connessione è una proprietà dello spazio
La connessione (connectedness) riguarda come è fatto lo spazio, cioè la sua struttura interna. Uno spazio topologico \( X \) è connesso se non può essere diviso in due parti disgiunte che siano entrambe aperte (o equivalenti, entrambe chiuse). È una proprietà intrinseca dello spazio, indipendente da qualsiasi funzione. - La continuità è una proprietà di una funzione
La continuità riguarda una funzione \( f: X \to Y \) tra due spazi topologici. Una funzione \( f \) è continua se l’immagine inversa di ogni insieme aperto di \( Y \) è un insieme aperto in \( X \). La continuità descrive come una funzione trasforma i punti, non com’è fatto lo spazio. Ad esempio, la funzione \( f(x) = x^2 \) è continua da \( \mathbb{R} \) in \( \mathbb{R} \) nella topologia standard, ma non dice nulla sul fatto che \( \mathbb{R} \) sia connesso o meno.
Ci sono teoremi che mettono in relazione connessione e continuità, ma non li identificano.
Ad esempio, se \( X \) è connesso e \( f: X \to Y \) è continua, allora l’immagine \( f(X) \) è connessa in \( Y \).
Questo mostra che la continuità preserva la connessione, ma non che siano la stessa cosa.
Note
Alcune note a margine sulla continuità topologica.
- Una funzione continua non è necessariamente aperta
Una funzione continua non necessariamente mappa insiemi aperti in insiemi aperti. Quindi, la continuità di una funzione non implica la preservazione degli insiemi aperti, a differenza di quanto avviene per le funzioni aperte. - Lemma dell'incollaggio
Date due funzioni continue \( f: A \to Y \) e \( g: B \to Y \) definite su due insiemi \( A \) e \( B \) che si sovrappongono e coincidono sulla loro intersezione, posso "incollarle" per ottenere una nuova funzione continua \( h \) definita sull'unione \( A \cup B \) dei due insiemi \( A \) e \( B \). - Funzione di inclusione
Se considero uno spazio topologico \( X \) e un sottoinsieme \( Y \) con una funzione di inclusione \( f \) che "inserisce" ogni punto di \( Y \) in \( X \), questa funzione è continua. - Topologia quoziente
Se considero una funzione suriettiva \( f \) da uno spazio topologico \( X \) a un insieme \( A \), la topologia quoziente su \( A \) è definita in modo tale che \( f \) sia continua. - Teorema della continuità della chiusura
La continuità preserva la relazione di appartenenza di un punto alla chiusura di un insieme. Se un punto $ x \in X $ appartiene alla chiusura di un insieme $ x \in Cl(A) $, dove $ A \subset X $ è un sottoinsieme di $ X $, la sua immagine $ f(x) $ appartiene alla chiusura dell'immagine f(A) ossia $ f(x) \in Cl(f(A)) $. - Definizione di continuità con gli insiemi aperti
La funzione è continua se e solo se, per ogni insieme aperto \( U \subset Y \) , la controimmagine \( f^{-1}(U) \) è un insieme aperto in \( X \). - Definizione di continuità con gli insiemi chiusi
La funzione \( f : X \to Y \) è continua se e solo se, per ogni insieme chiuso \( C \subset Y \) , la controimmagine \( f^{-1}(C) \) è un insieme chiuso in \( X \). - Teorema della composizione di funzioni continue.
Se due funzioni \( f \) e \( g \) sono continue, allora anche la loro composizione g∘f è continua. - Teorema della continuità tramite sequenze
Il teorema afferma che se una funzione \( f: X \to Y \) è continua e una sequenza di punti \( x_1, x_2, \dots \) in \( X \) converge a un punto \( x \), allora la sequenza dei valori delle immagini \( f(x_1), f(x_2), \dots \) converge al valore \( f(x) \) in \( Y \). - Funzioni polinomiali
In uno spazio topologico \(\mathbb{R}\) con la topologia standard, ogni funzione polinomiale \(p : \mathbb{R} \to \mathbb{R}\), con \(p(x) = a_nx^n + \dots + a_1x + a_0\), è continua.
E così via.
