Topologia quoziente

Sia $X$ uno spazio topologico e $A$ un insieme che non è necessariamente un sottoinsieme di $X$. Sia $p: X \rightarrow A$ una mappa suriettiva. Un sottoinsieme $U$ di $A$ è aperto in $A$ se e solo se $p^{-1}(U)$ è aperto in $X$.

In altre parole, se l'insieme $U$ in $A$ è aperto nella topologia quoziente su $A$ allora anche la preimmagine $p^{-1}(U)$ di $U$ sotto la mappa $p$, ovvero l'insieme dei punti di $X$ che $p$ manda in $U$, è un insieme aperto in $X$.

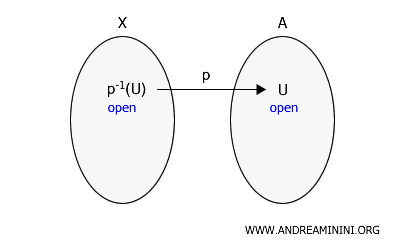
la topologia quoziente

Questa definizione è utilizzata per definire una nuova topologia su $A$ chiamata topologia quoziente, che è indotta dalla topologia di $X$ attraverso la mappa $p$.

L'insieme A è chiamato spazio quoziente mentre la mappa p è chiamata mappa quoziente.

La collezione di insiemi aperti in $ A $ è anche detta "topologia quoziente indotta da p".

Questo vuol dire che nella topologia quoziente sono definiti aperti gli insiemi che hanno come preimmagine un insieme aperto nello spazio di origine.

È importante chiarire un errore comune:

La preimmagine di un insieme aperto nel quoziente A è aperta nello spazio d'origine X. Ma non vale l'inverso.
L'immagine di un insieme aperto nello spazio d'origine X non è necessariamente aperta nel quoziente A, perché la mappa $p: X \rightarrow A$ potrebbe distorcerlo, ossia "schiacciarlo" sul quoziente A.

Quindi, uno spazio quoziente è uno spazio topologico ottenuto a partire da un altro spazio topologico, identificando o "incollando" insieme certi punti secondo una relazione di equivalenza.

In parole più semplici, lo spazio quoziente è il risultato di "incollare" (ossia raggruppare) insieme i punti di uno spazio secondo una certa regola e poi studiare le proprietà topologiche dello spazio risultante.

Ma perché ci interessa la topologia quoziente? Creare una topologia quoziente mi permette di studiare come si comporta lo spazio A (spazio quoziente) che potrebbe essere più difficile o complesso, usando le informazioni che ho su X (spazio di origine) che spesso è più semplice da analizzare.

Spiegazione
Un esempio pratico
Le proprietà della topologia quoziente

Spiegazione

Il concetto di "topologia quoziente" può essere complesso, ma cercherò di spiegarto in modo più semplice.

La "topologia quoziente" è un modo per trasformare questa forma in una nuova forma incollando insieme alcuni dei suoi bordi o lati.

Ad esempio, prendo un foglio di forma quadrata. Se incollo i due lati opposti tra loro posso formare un cilindro.

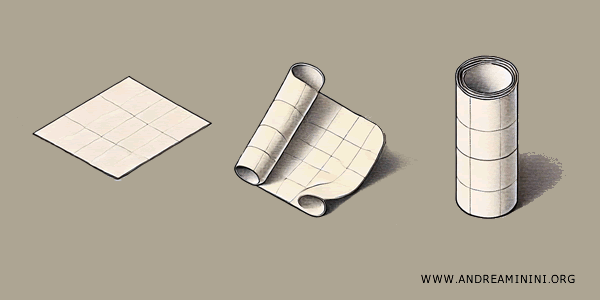
piego il foglio su se stesso

Se poi incollo insieme i bordi circolari del cilindro ottengo una ciambella o un toro.

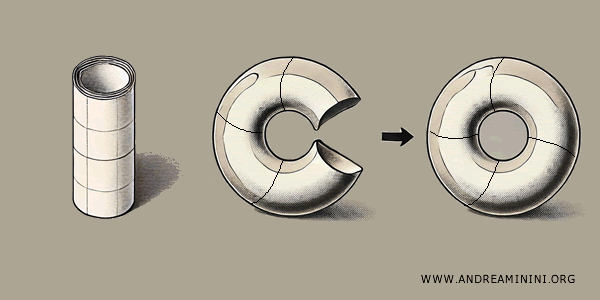
esempio di toro

In questo esempio, il quadrato viene trasformato prima in un cilindro e poi in un toro (una ciambella) incollando i lati opposti.

Allo stesso modo, la topologia quoziente mi permette di creare nuove forme o spazi topologici a partire da forme più semplici, "incollando" alcune parti insieme.

Questo concetto è molto usato in matematica per studiare le proprietà delle superfici e degli spazi in un modo più astratto.

Un esempio pratico

Considero lo spazio topologico $ X = [0, 1] $ con la topologia usuale, dove gli insiemi aperti sono intervalli aperti o unioni di intervalli aperti.

In questo spazio:

L'insieme $ X $ e l'insieme vuoto $ \emptyset $ sono aperti per definizione.
Ogni intervallo aperto $ (a,b) $ con $ 0 \leq a < b \leq 1 $ è aperto in $ X $.

Lo spazio $ X $ può essere visto come un segmento con un estremo in $ 0 $ e l'altro in $ 1 $.

esempio di segmento [0,1]

Ora, costruisco un nuovo spazio quoziente incollando insieme i punti $ 0 $ e $ 1 $ dell'intervallo $[0, 1]$. In pratica, sto "identificando" $ 0 $ e $ 1 $ come se fossero lo stesso punto.

Per fare questo, definiamo una mappa $ p: [0, 1] \rightarrow A $ come segue:

$$ p(x) = \begin{cases} p(0) & \text{se } x = 0 \text{ o } x = 1 \\ \\ x & \text{se } 0 < x < 1 \end{cases} $$

Il nuovo insieme quoziente $ A $ che otteniamo, identificando $ 0 $ e $ 1 $, può essere visto come un cerchio, dove i punti $ 0 $ e $ 1 $ sono stati "incollati" insieme.

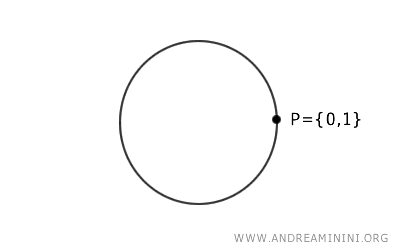
la topologia quoziente

In altre parole, ho "curvato" il segmento fino a congiungere gli estremi 0 e 1 tra loro.

Nel nuovo spazio $ A $, il punto $ P = \{0, 1\} $ è l'immagine sia del punto $ 0 $ che del punto $ 1 $ di $ X $ tramite la mappa $ p $.

Ora, per definire la topologia su $ A $, devo decidere quali insiemi in $ A $ saranno considerati aperti.

Secondo la definizione di topologia quoziente, un insieme $ U \subseteq A $ è aperto in $ A $ se la sua preimmagine $ p^{-1}(U) $ è un insieme aperto in $ [0, 1] $.

Vediamo i due casi:

Intervallo $ U = (a,b) $ che non contiene $ P $
La sua preimmagine in $ X $ è l'intervallo $ (a,b) $, che è aperto in $ X $. Di conseguenza, $ U $ è aperto in $ A $.
Intervallo $ U = (a,b) $ che contiene $ P = \{0,1\} $
La preimmagine in $ X $ è l'unione di due intervalli $ [0,a) \cup (b,1] $, entrambi aperti in $ X $. Quindi, $ U $ è aperto in $ A $.

In questo modo, ho creato un nuovo spazio topologico $ A $, che è un cerchio, a partire da uno spazio più semplice, l'intervallo $ [0, 1] $.

Questo è un classico esempio di come la topologia quoziente può trasformare uno spazio semplice in una forma più complessa.

Esempio 2

In questo esempio di topologia quoziente voglio "arrotolare" la retta reale su un cerchio

Considero la retta reale ($ \mathbb{R} $) che si estende all'infinito in entrambe le direzioni.

Ora, voglio "arrotolare" la retta reale su un cerchio, identificando ogni punto reale con la sua posizione frazionaria.

Questo si fa con una mappa che chiamo $ p(x) = x \mod 1 $.

Cosa significa? Semplice: per ogni numero reale $ x $, prendo solo la sua parte decimale (la parte dopo la virgola) e uso quella per rappresentare il punto su un cerchio.

Ad esempio, se $ x = 1.3 $ la mappa prende la parte decimale 0.3 e la mette in corrispondenza di un punto sul cerchio. Se $ x = 2.7 $, la sua parte decimale è 0.7, quindi sarà lo stesso punto del cerchio che ottengo da $ 0.7 $.
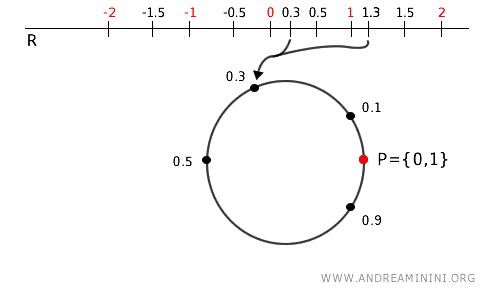
esempio

Ogni volta che il valore $ x $ aumenta di un intero (ad esempio, da 1.3 a 2.3 o a 3.3), il punto finisce sempre nello stesso punto sul cerchio.

Questo è ciò che intendo per "arrotolare" la retta sul cerchio dove i punti 0 e 1 coincidono..

A questo punto considero vari intervalli.

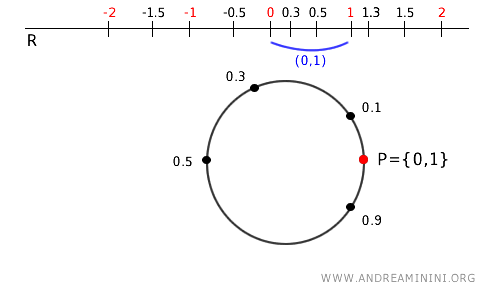
Intervallo (0,1) su R
L'intervallo $ (0, 1) $ su R si arrotola su un arco del cerchio. Non include però il punto 0 del cerchio. Posso affermare che l'intervallo (0,1) è aperto nello spazio quoziente (il cerchio) perché la sua preimmagine (0,1) è aperta nello spazio di origine (R).
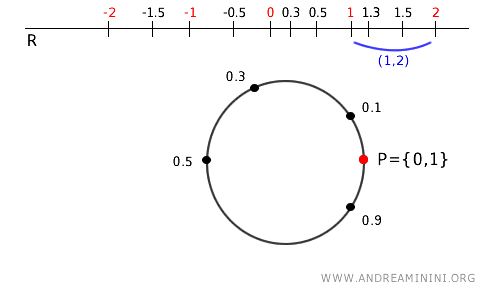
Intervallo (1,2) su R
L'intervallo $ (1, 2) $ su R si arrotola di nuovo sullo stesso arco, perché $ 1 $ e $ 2 $ vengono identificati con 0 (cioè, $ 1 \mod 1 = 0 \mod 1 $). In altre parole, l'intervallo (1,2) su R ha come immagine ancora l'intervallo (0,1) sul cerchio che già so essere "aperto" nella topologia quoziente. Pertanto, non aggiunge nulla a quello che già conosco.
Intervallo (0,2) su R
L'intervallo $ (0, 2) $ sulla retta reale è un intervallo aperto. Questo intervallo va da 0 a 2, ma cosa succede quando lo arrotolo sul cerchio usando la mappa $ p $? L'intervallo $ (0, 2) $ copre tutto il cerchio perché include anche 1 e si arrotola due volte sugli stessi archi di cerchio. Quindi, l'intervallo $ (0, 2) $ sulla retta copre tutto il cerchio. Anche se $ (0, 2) $ è aperto sulla retta reale, l'immagine che ottengo dopo averlo arrotolato è tutto il cerchio, che in questo caso è sia aperto che chiuso (clopen). In un cerchio, non c’è un vero bordo, quindi l’intero cerchio è considerato aperto e chiuso allo stesso tempo.

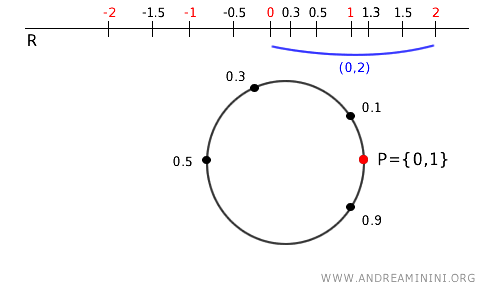
Nota. Questo dimostra che un insieme aperto nello spazio di origine non necessariamente ha per immagine un insieme aperto nello spazio quoziente.

In generale, se prendo un insieme aperto sul cerchio, la sua preimmagine sulla retta reale sarà sempre aperta.

Questo funziona perché ogni volta che "srotolo" un insieme aperto dal cerchio alla retta, ottengo degli intervalli aperti.

Ma non vale l'inverso, se prendo un insieme aperto sullo spazio di origine, non è detto che la sua immagine sia aperta nello spazio quoziente.

Morale della storia

Non posso sempre dire che un insieme aperto sulla retta reale avrà un’immagine aperta sul cerchio, perché la mappa che arrotola può "schiacciare" o "comprimere" gli insiemi, cambiando il loro comportamento topologico.

Esempio 3

In questo esercizio provo a ottenere una topologia quoziente unendo il primo ( $ m $) e l'ultimo numero ($ n $)in una serie di numeri interi consecutivi $ \{ m, m+1, ..., n ) di $ \mathbb{Z} $.

Considero la serie di 7 numeri interi consecutivi da 1 a 7.

$$ I_7 = \{1, 2, 3, 4, 5, 6, 7\} $$

Si tratta di un intervallo digitale perché è composto da numeri interi consecutivi.

Ora, unisco il primo numero (1) con l'ultimo numero (7). È come se prendessi una linea retta e collegassi le sue estremità per formare un anello o cerchio.

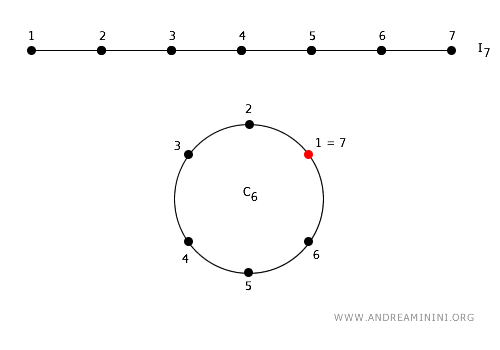
esempio di cerchio digitale

In questo modo ottengo una nuova struttura topologica che si chiama cerchio digitale $ C_6 $ composto da 6 punti.

Ogni punto ha una relazione di adiacenza con altri due punti del cerchio digitale.

Si tratta di una topologia quoziente, perché ho creato un nuovo spazio topologico diverso a partire dall'intervallo digitale di origine.

Nota. Il risultato è una forma simile al cerchio ottenuto unendo gli estremi in un intervallo reale (a,b). In questo caso, però, è composto da numeri interi ovvero da un numero finito di punti.

Il cerchio digitale è anche un esempio di topologia digitale, perché ogni punto ha una relazione con i punti vicini.

Pertanto, è uno spazio discreto in cui posso applicare i concetti della topologia digitale, come la connessione e la definizione di insiemi aperti digitali.

Nota. In una topologia digitale un insieme U è aperto se ogni punto x∈U dell'insieme include anche i suoi punti confinanti o vicini, (secondo il tipo di connessione scelto, come la 2-connessione in un cerchio o in un anello (1D), la 4-connessione o l'8-connessione sul piano (2D), o la 6-connessione o la 18-connessione nello spazio (3D).

Va però specificato che la topologia quoziente e la topologia digitale sono topologie diverse.

In altre parole, il fatto che il cerchio digitale possa essere ottenuto come una topologia quoziente non lo esclude dalla classificazione anche come topologia digitale, ma queste due topologie non vanno confuse tra loro.

Esempio 4

Considero l'insieme dei numeri reali $ \mathbb{R} $ con la topologia standard e una mappa quoziente $ p: \mathbb{R} \to \{a, b, c\} $ definita così:

$$ p(x) = \begin{cases} = a \ \ se \ \ x < 0 \\ \\ = b \ \ se \ \ x = 0 \\ \\ = c \ \ se \ \ x > 0 \\ \\ \end{cases} $$

Quindi sto fondamentalmente schiacciando tutto l’intervallo dei numeri negativi in $ a $, il punto $ 0 $ in $ b $, e tutto l’intervallo positivo in $ c $.

La topologia quoziente indotta da questa mappa dipende dalle preimmagini degli elementi $ a $, $ b $, e $ c $.

Le preimmagini sono:

$ p^{-1}(a) = (-\infty, 0) $, che è un insieme aperto in $ \mathbb{R} $,
$ p^{-1}(b) = \{0\} $, che **non** è aperto in $ \mathbb{R} $,
$ p^{-1}(c) = (0, \infty) $, che è aperto in $ \mathbb{R} $.

Sapendo che nella topologia quoziente, un insieme in $ \{a, b, c\} $ è aperto se la sua preimmagine sotto $ p $ è aperta in $ \mathbb{R} $, posso stabilire che i seguenti insiemi sono aperti nella topologia quoziente:

Il sottoinsieme $ \{a\} $ è aperto perché la sua preimmagine $ (-\infty, 0) $ è aperta in $ \mathbb{R} $.
Il sottoinsieme $ \{c\} $ è aperto perché la sua preimmagine $ (0, \infty) $ è aperta in $ \mathbb{R} $.
L’unione $ \{a, c\} $ è aperta perché la preimmagine $ (-\infty, 0) \cup (0, \infty) = \mathbb{R} \setminus \{0\} $ è aperta in $ \mathbb{R} $.

Sono aperti nella topologia quoziente anche l'insieme totale e l'insieme vuoto

L'insieme totale, cioè tutto lo spazio {a,b,c}, è sempre aperto in qualsiasi topologia quoziente, perché la preimmagine di {a,b,c} sotto la mappa p è l'insieme totale di R che per definizione è aperto nella sua topologia standard.
L'insieme vuoto ∅ è l'altro caso base ed è sempre aperto. La preimmagine dell'insieme vuoto sotto p è ancora l'insieme vuoto in R che per definizione è aperto in qualsiasi topologia.

Il sottoinsieme $ \{b\} $ invece non è aperto nella topologia quoziente, perché la sua preimmagine $ \{0\} $ non è aperta in $ \mathbb{R} $.

In conclusione, la topologia quoziente su $ \{a, b, c\} $ ha gli insiemi $ \emptyset $, $ \{a,b,c \} $, $ \{a\} $, $ \{c\} $, e $ \{a, c\} $ come aperti, ma $ \{b\} $ non è aperto perché il punto $ 0 $ sulla retta reale non è aperto.

Praticamente, $ b $ è una "singolarità", un punto isolato che non riesco a tirare fuori come aperto.

Le proprietà della topologia quoziente

Alcune proprietà della topologia quoziente utili da sapere

L'insieme vuoto e l'insieme quoziente sono insiemi aperti nella topologia quoziente
Sia l'insieme vuoto che l'intero insieme quoziente sono aperti nella topologia quoziente.
- Preimmagine dell'insieme vuoto
  La preimmagine dell'insieme vuoto $ p^{-1}(\emptyset) $ tramite la mappa $ p $ è ancora l'insieme vuoto $ \emptyset $, che è un insieme aperto in $ X $. Quindi $ \emptyset $ è aperto nella topologia quoziente.
- Preimmagine dell'insieme totale
  La preimmagine di un insieme $ A $ tramite $ p $ è l'intero insieme $ X $, che è aperto in $ X $. Di conseguenza, anche l'insieme $ A $ è aperto nella topologia quoziente.
Nota. In altre parole, l'insieme vuoto e l'intero insieme sono sempre aperti in qualsiasi topologia, quindi anche le loro immagini nella topologia quoziente lo saranno. L'immagine dell'insieme vuoto tramite la mappa $ p: X \rightarrow A $ è ancora $ \emptyset $, mentre l'immagine dell'intero insieme $ X $ è l'insieme $ A $.
Unione di insiemi aperti nella topologia quoziente
Se $ U_i $ è aperto nella topologia quoziente su $ A $, allora la sua preimmagine sotto $ p $ è aperta in $ X $. Di conseguenza, l'unione di insiemi aperti in $ A $ ha come preimmagine un'unione di insiemi aperti in $ X $: $$
\left( \forall i, \ U_i \text{ è aperto in } A \right) \Rightarrow p^{-1}\left( \bigcup U_i \right) = \bigcup p^{-1}(U_i) \text{ è aperto in } X $$ Quindi, l'unione arbitraria di insiemi aperti nella topologia quoziente rimane aperta in $ A $.
Nota: L'unione di insiemi aperti $ \bigcup U_i $ nella topologia quoziente $ A $ è ancora un insieme aperto. Ciò implica che anche la preimmagine dell'unione $ p^{-1}( \bigcup U_i ) $ è un insieme aperto in $ X $. La preimmagine di un'unione è l'unione delle preimmagini, cioè $ p^{-1}\left( \bigcup U_i \right) = \bigcup p^{-1}(U_i) $, e dato che ciascuno $ p^{-1}(U_i) $ è aperto in $ X $, anche l'unione delle preimmagini è aperta in $ X $. In conclusione, poiché la preimmagine di $ \bigcup U_i $ è aperta in $ X $, questo significa che $ \bigcup U_i $ è aperto nella topologia quoziente su $ A $. Pertanto, la nozione di apertura si trasferisce attraverso la mappa quoziente $ p $.
Intersezione di insiemi aperti nella topologia quoziente
Se gli insiemi U_i sono aperti nello spazio quoziente, allora l'intersezione delle loro preimmagini è aperta nello spazio d'origine X.
Nota. In altre parole $ U_i $ sono insiemi aperti nel quoziente $ A $. La mappa quoziente $ p: X \to A $ ha la proprietà che la preimmagine di un insieme aperto nel quoziente è aperta in $ X $. Quindi, ogni preimmagine $ p^{-1}(U_i) $ è aperta nello spazio d'origine $ X $. L'intersezione finita di insiemi aperti in $ X $ è ancora aperta, quindi $ \bigcap p^{-1}(U_i) $ sarà aperta in $ X $. In conclusione, se gli insiemi sono aperti nello spazio quoziente, allora l'intersezione delle loro preimmagini è aperta nello spazio d'origine.

E così via.