Spazio Hausdorff

Uno spazio di Hausdorff è uno spazio topologico in cui per ogni coppia di punti distinti esistono intorni aperti disgiunti che li separano.

In altre parole, se prendo due punti qualsiasi $ x $ e $ y $ in uno spazio di Hausdorff, posso trovare un intorno aperto $ U $ contenente $ x $ e un intorno aperto $ V $ contenente $ y $ tali che gli intorni $ U $ e $ V $ non hanno punti in comune, ovvero, $ U \cap V = \emptyset $.

Questa proprietà assicura che lo spazio abbia una forma di "separabilità", dando una nozione di distanza e vicinanza tra i punti che è simile a quella intuitiva nella geometria euclidea.

Gli spazi di Hausdorff sono molto apprezzati nell'analisi e nella geometria, poiché facilitano il trattamento della convergenza delle sequenze di punti

Una proprietà importante è che in uno spazio Hausdorff i sottoinsiemi costituiti da un solo punto sono insiemi chiusi.

Questo significa che il complementare di un punto singolo, cioè l'insieme di tutti gli altri punti tranne quello, è sempre un insieme aperto.

Esempio pratico
Osservazioni

Esempio pratico

Esempio 1

Considero l'insieme dei numeri reali R e la topologia standard, quella che è comunemente usata per rappresentare la retta reale $\mathbb{R}$.

esempio linea dei numeri reali

La topologia standard su R considera come insieme aperto ogni possibile unione di intervalli aperti (a,b) con a<b e ogni intersezione di un numero finito di insiemi aperti.

Quindi, in questa topologia i singoli punti {x} non sono insiemi aperti.

Spiegazione. Un insieme aperto in questa topologia è definito come un insieme che, per ogni punto al suo interno, contiene un intero intervallo aperto intorno a quel punto, perché tra due numeri reali qualsiasi esitono infiniti altri numeri reali. I singoli punti $ \{x\} $ non soddisfano questa condizione perché non c'è spazio intorno a un singolo punto che possa essere contenuto all'interno dell'insieme senza includere altri punti. Quindi, nella topologia standard sulla retta reale i singoli punti non sono aperti.

Il complementare di ogni singolo punto $ \mathbb{R} \setminus \{x\} $ è, invece, un insieme aperto.

l'intorno del punto singolo è un insieme aperto

Da questo deduco che ogni singolo punto $ \{x\} $ è un insieme chiuso perché il suo complementare è un insieme aperto.

La topologia standard è anche uno spazio di Hausdorff perché dato un qualsiasi paio di punti distinti $ a $ e $ b $ su $\mathbb{R}$, è sempre possibile trovare due intervalli aperti, uno intorno ad $ a $ e l'altro intorno a $ b $, che non si sovrappongono.

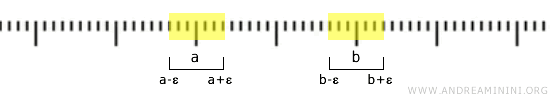
gli intorni dei punti a e b

Ad esempio, se $ a < b $, possiamo prendere gli intervalli $ (a-\epsilon, a+\epsilon) $ e $ (b-\epsilon, b+\epsilon) $ per un $ \epsilon $ sufficientemente piccolo in modo che $ a+\epsilon < b-\epsilon $, garantendo che gli intervalli siano disgiunti.

Poiché la topologia standard sulla retta reale è anche uno spazio Hausdorff, il fatto che i singoli punti nella topologia standard sono insiemi chiusi è in linea con la definizione di spazio Hausdorff.

Esempio 2

Considero uno spazio topologico composto dall'insieme X = {1,2,3} nella topologia discreta

Nella topologia discreta ogni elemento (punto) di X è considerato aperto.

Di conseguenza, sono aperti tutti i possibili sottoinsiemi di $ X $.

L'insieme vuoto $ \emptyset $
Gli insiemi singoletti $ \{1\} $, $ \{2\} $, $ \{3\} $
Gli insiemi con due elementi $ \{1, 2\} $, $ \{1, 3\} $, $ \{2, 3\} $ per unione/intersezione di insiemi aperti
L'insieme stesso $ \{1, 2, 3\} $

In totale, ci sono $ 2^3 = 8 $ insiemi aperti, corrispondenti a tutti i sottoinsiemi di $ X $.

Questo spazio topologico con la topologia discreta è sempre uno spazio di Hausdorff.

Questo perché, per definizione, uno spazio è di Hausdorff se per ogni coppia di punti distinti $ x $ e $ y $ esistono due intorni aperti $ U $ e $ V $ tali che $ U \cap V = \emptyset $ e $ x \in U $, $ y \in V $.

In questo spazio topologico se prendo due punti distinti $ x $ e $ y $ in $ X = \{1, 2, 3\} $, posso semplicemente scegliere gli intorni $ U = \{x\} $ e $ V = \{y\} $.

Chiaramente, questi due intorni sono disgiunti $ U \cap V = \emptyset $ soddisfacendo così la condizione per essere uno spazio di Hausdorff.

Ad esempio, se scelgo i punti x={1} e y={2} e come intorno U={1} e V={2}, l'intersezione tra {1} e {2} è l'insieme vuoto.

$$ \{ 1 \} \cap \{ 2 \} = \emptyset $$

Questo vuole dire che i due elementi hanno un intorno che non si sovrappone.

Lo stesso accade scegliendo qualsiasi altra coppia di elementi di X.

Nella topologia discreta i singoli punti sono insiemi aperti o chiusi? La prima volta che ho svolto questo esercizio mi è sorto un dubbio. Se la topologia discreta è uno spazio di Hausdorff, allora i singoli punti {x} dovrebbero essere chiusi, ma in questo caso sono aperti per definizione stessa della topologia discreta. Perché?

La risposta a questo dubbio è molto semplice anche se inizialmente potrebbe sembrare controintuitiva: in topologia un insieme può essere sia aperto che chiuso, tali insiemi sono spesso chiamati insiemi clopen. In altre parole, in topologia "chiuso" non è l'opposto di "aperto".

Nella topologia discreta ogni singolo punto {x} è anche un insieme chiuso perché il suo complementare, che è l'insieme di tutti gli altri punti diversi da x è un'unione di insiemi aperti ed è quindi un insieme aperto.

Pertanto, se il complementare del singolo punto {x} è un insieme aperto, deduco che il singolo punto {x} è anche un insieme chiuso.

Ad esempio, considerando l'insieme X={1,2,3}, se prendo l'elemento {1} questo è un insieme aperto per definizione stessa della topologia discreta. Tuttavia è anche un insieme chiuso perché il suo complementare X/{1}={2,3} è un insieme aperto. Il complementare di un insieme aperto è sempre un insieme chiuso.

Riepilogando, i singoli punti {x} della topologia discreta sono sia aperti che chiusi.

Aperti
Nella topologia discreta ogni singolo punto è un insieme aperto per definizione stessa della topologia.
Chiusi
Il complementare X/{x} di un singolo punto {x} è l'insieme di tutti gli altri punti/elementi di X che non sono nel sottoinsieme {x}. Poiché nella topologia discreta tutti i singoli punti sono aperti, ne deduco che anche la loro unione è un insieme aperto. Quindi, l'insieme complementare X/{x} è un insieme aperto. Poiché il complementare di {x} è un insieme aperto, deduco che l'insieme {x} è un insieme chiuso.

In sintesi, i singoli punti {x} sono aperti perché ogni sottoinsieme è aperto nella topologia discreta, e sono chiusi perché i loro complementari sono aperti.

Un'importante differenza tra la topologia discreta e quella standard è che nella topologia standard, non tutti i sottoinsiemi sono aperti. Solo quelli che rispettano la definizione di "intorno aperto" per ogni punto contenuto nell'insieme sono considerati aperti.

Osservazioni

Alcune osservazioni e note a margine sugli spazi di Hausdorff

In uno spazio di Hausdorff ogni successione convergente di punti converge a un unico punto
In uno spazio di Hausdorff X ogni successione convergente di punti converge a un unico punto x∈X, perché se convergesse a due o più punti distinti, questi avrebbero due intorni non più disgiunti tra loro.
Dimostrazione. Considero uno spazio di Hausdorff X (ad esempio uno spazio reale X=R). Per assurdo ipotizzo che una successione convergente di punti x₁,x₂,x₃,..., converge a due punti distinti x e y dello spazio X. Secondo la definizione di convergenza di una successione di punti, questo significa che esiste un numero intero N tale che per ogni n>N i punti x_n appartengono all'intorno A di x.

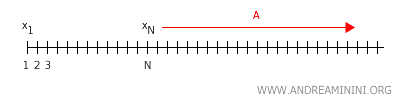
D'altra parte esiste anche un numero intero M tale che per ogni n>M i punti x_n appartengono all'intorno B di y.

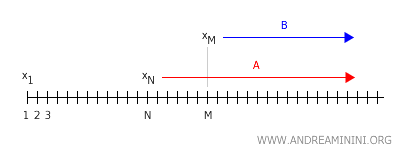
Se M>N una parte dei punti dell'intorno A di x appartiene anche all'intorno B di y. Lo stesso accadrebbe se N>M, in questo caso una parte dei punti dell'intorno B di y apparterrebbe anche all'intorno A di x. In entrambi i casi, l'intersezione tra i due intorni dei punti x e y non sarebbe vuota $$ A \cap B \not = \emptyset $$ I due intorni A e B non sono disgiunti. Questo contraddice una proprietà fondamentale degli spazi di Hausdorff, quella per cui in ogni coppia x e y di punti distinti dello spazio X esistono intorni aperti disgiunti ($ A \cap B = \emptyset $). Pertanto, in uno spazio di Hausdorff una successione convergente di punti non può convergere a due o più punti distinti. Questa ipotesi è falsa. Di conseguenza, in uno spazio di Hausdorff una successione convergente può convergere soltanto a un unico punto x dello spazio X.

E così via.