Intorno circolare aperto
In topologia una open ball (intorno circolare, disco o palla aperta) è l'insieme di tutti i punti che si trovano all'interno di una distanza specificata, detta raggio (r), da un punto fisso detto centro (c). $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$
Dove \( M \) è uno spazio metrico e \( d \) è una metrica, ossia una funzione che definisce la distanza tra due punti nello spazio.
Ogni open ball è sempre caratterizzata da un centro e un raggio.
Sono "aperte" nel senso topologico, il che significa che per ogni punto all'interno dell'interno circolare, c'è un intorno circolare più piccolo completamente contenuto in quello più grande.
Nota. Le palle aperte sono invarianti rispetto a omoteticità (cambiamenti di scala) e traslazioni (spostamenti), nel senso che queste operazioni producono ancora una palla aperta.
Ad esempio, nel piano R2 la formula euclidea permette di calcolare la distanza di un punto p=(x,y) da un altro punto c=(x0,y0) scelto come centro.
$$ d(p,c) = \sqrt{(x-x_0)^2+(y-y_0)^2} $$
Gli intorni circolari aperti sono utilizzati per definire la struttura di uno spazio topologico nel piano e come una base per una topologia.
La topologia standard nel piano R2 è una base composta da una collezione di open ball.
$$ B = \{ B(p, r) \ | \ p \in R^2 \ , \ r > 0 \} $$
Dove p è un punto p=(x,y) dello spazio bidimensionale ed r è il raggio dell'intorno circolare.

Non è l'unica topologia del piano ma è sicuramente quella più comune.
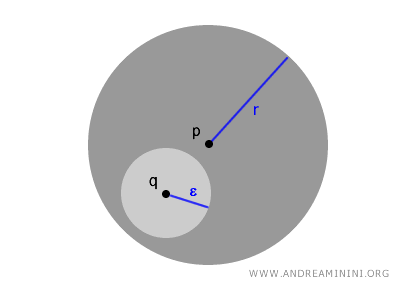
Essendo una open ball, ogni punto $ q \in B(p,r) $ è a sua volta contenuto in una open ball più piccola B(q,ε) centrata in q e interamente contenuta in B(p,r).
$$ \forall \ q \in B(p,r) \ \exists \ \epsilon > 0 \ | \ B(q,ε)⊂ B(p,r) $$
E così via.
