Definizione di continuità con gli insiemi aperti

La funzione $ f : X \to Y $ è continua se e solo se, per ogni punto $ x \in X $ e per ogni insieme aperto $ U \subset Y $ che contiene $ f(x) $, esiste un intorno $ V $ di $ x $ tale che $ f(V) \subset U $.

In altre parole, la funzione $ f: X \to Y $ è continua se, per ogni insieme aperto $ U \subset Y $, la controimmagine $ f^{-1}(U) $ è un insieme aperto in $ X $.

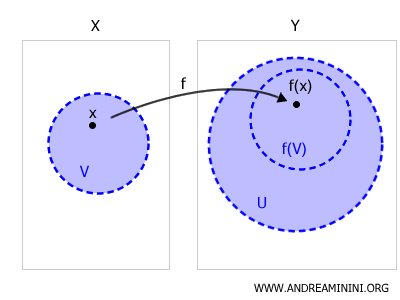
esempio

La continuità di una funzione implica che la preimmagine di qualsiasi insieme aperto del codominio sia sempre un insieme aperto nel dominio.

Pertanto, il teorema introduce una definizione topologica di continuità della funzione, che si basa sugli insiemi aperti nel dominio e nel codominio.

E' anche conosciuta come definizione di continuità con gli insiemi aperti.

Nota. Questo teorema è anche detto di "equivalenza delle definizioni di continuità" perché stabilisce che le due definizioni di continuità per una funzione, quella con gli insiemi aperti (topologica) e quella analitica con $\varepsilon$-$\delta$ (analitica), sono equivalenti tra loro. Dove per definizione analitica di continuità intendo la seguente: "Una funzione $ f $ è continua in un punto $ x_0 \in \mathbb{R} $ se, per ogni $\varepsilon > 0$, esiste un $\delta > 0$ tale che, per ogni $ x \in \mathbb{R} $, se $ |x - x_0| < \delta $, allora $ |f(x) - f(x_0)| < \varepsilon $" che normalmente si studia nei corsi base di analisi matematica.

Vale anche il contrario, la definizione di continuità può essere definita anche con gli insiemi chiusi.

Dati due spazi topologici $ X $ e $ Y $, una funzione $ f: X \to Y $ è continua se e solo se la controimmagine $ f^{-1}(C) $ di ogni insieme chiuso in $ Y $ è un insieme chiuso in $ X $.

Quindi, la nozione di continuità posso esprimerla indifferentemente in termini di insiemi aperti o chiusi, perché le proprietà di chiusura e apertura sono strettamente collegate nelle topologie.

Un esempio pratico
Dimostrazione

Un esempio pratico

Considero la funzione $ f : \mathbb{R} \to \mathbb{R} $ definita come $ f(x) = x^2 $.

Devo capire se questa funzione è continua oppure no utilizzando la definizione con gli insiemi aperti del teorema.

Secondo la definizione di continuità con insiemi aperti:

La funzione $ f $ è continua se, per ogni insieme aperto $ U \subset \mathbb{R} $ e per ogni $ x \in f^{-1}(U) $, esiste un intorno $ V $ di $ x $ tale che $ f(V) \subset U $.

Scelgo un insieme aperto $ U \subset \mathbb{R} $.

Ad esempio, prendo l'insieme aperto $ U = (1, 4) $, cioè tutti i numeri tra 1 e 4.

esempio di insieme aperto

Voglio capire se $ f^{-1}(U) $, cioè l'insieme dei numeri in $ \mathbb{R} $ che vengono mandati nell'intervallo $ (1, 4) $ da $ f(x) = x^2 $, è aperto.

Per trovare $ f^{-1}(U) $, devo vedere quali numeri $ x $ soddisfano $ x^2 \in (1, 4) $. In altre parole, voglio trovare gli $ x $ tali che:

$$ 1 < x^2 < 4 $$

Da questa disequazione ottengo che:

$$ 1 < |x| < 2 $$

Quindi, $ x $ deve appartenere all'intervallo $ (-2, -1) \cup (1, 2) $.

Questo è l'insieme $ f^{-1}(U) $, che è chiaramente un insieme aperto in $ \mathbb{R} $.

A questo punto verifico la continuità.

Scelgo un punto qualsiasi $ x \in f^{-1}(U) $ dove $ U = (1, 4) $. Ad esempio, il punto $ x = 1.5 $.

L'immagine di $ x=1.5 $ è $ f(1.5) = 1.5^2 = 2.25 $, che appartiene all'intervallo $ U = (1, 4) $.

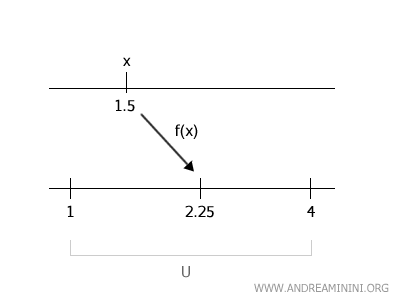
esempio

Devo trovare un intorno $ V $ di $ x = 1.5 $ tale che $ f(V) \subset (1, 4) $.

Scelgo un piccolo intervallo intorno a $ 1.5 $, per esempio $ V = (1.4, 1.6) $.

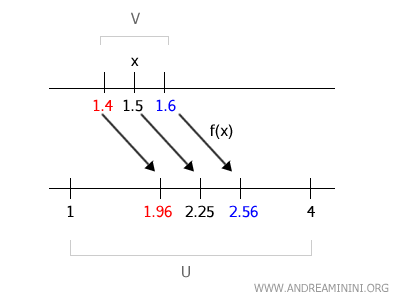
esempio

Se calcolo i valori di $ f(x) = x^2 $ per $ x \in (1.4, 1.6) $, ottengo che:

$$ f(1.4) = 1.4^2 = 1.96 \quad \text{e} \quad f(1.6) = 1.6^2 = 2.56 $$

L'intervallo $ f(V) = (1.96, 2.56) $ è contenuto nell'intervallo aperto $ U = (1, 4) $.

$$ f(V) \subset U $$

Questo dimostra che per ogni punto $ x \in f^{-1}(U) $, esiste un intorno $ V $ di $ x $ tale che $ f(V) \subset U $ che soddisfa la definizione della continuità.

Lo stesso accade se prendo qualsiasi altro punto $ x \in \mathbb{R} $, confermando che la funzione $ f(x) = x^2 $ è continua secondo la definizione di continuità degli insiemi aperti.

Nota. La condizione di continuità deve essere verificata per tutti i punti $ x \in \mathbb{X} $. Non basta controllare che la condizione sia soddisfatta per un solo punto $ x $. Questo perché la continuità di una funzione è una proprietà globale, che deve valere in ogni punto del dominio. Quindi, per dimostrare che una funzione $ f : \mathbb{R} \to \mathbb{R} $ è continua, devo dimostrare che per ogni punto $ x \in \mathbb{R} $ e per ogni insieme aperto $ U $ contenente $ f(x) $, esiste un intorno $ V $ di $ x $ tale che $ f(V) \subset U $.

Dimostrazione

La dimostrazione divisa in due parti:

A] Prima parte

Per ipotesi iniziale la funzione $ f $ è continua secondo la definizione degli insiemi aperti.

Scelgo un punto $ x \in X $ e un insieme aperto $ U \subset Y $ tale che $ f(x) \in U $.

Ora definisco $ V = f^{-1}(U) $, cioè l'insieme di tutti i punti in $ X $ che vengono mandati dentro $ U $ da $ f $.

Poiché $ f $ è continua secondo la definizione degli insiemi aperti, deduco che $ V $ è un insieme aperto in $ X $.

Quindi, poiché $ x \in V $ e $ f(V) \subset U $, ho dimostrato che per ogni aperto $ U $ in $ Y $ contenente $ f(x) $, esiste un aperto $ V $ in $ X $ contenente $ x $.

B] Seconda parte

Per ipotesi iniziale per ogni punto $ x \in X $ e per ogni insieme aperto $ U \subset Y $ contenente $ f(x) $, esiste un intorno $ V $ di $ x $ tale che $ f(V) \subset U $.

Devo dimostrare che $ f^{-1}(W) $ è aperto in $ X $ per ogni insieme aperto $ W \subset Y $.

In altre parole, devo dimostrare che l'insieme dei punti in $ X $ che vengono mandati in $ W $ da $ f $ è aperto.

Prendo un punto $ x \in f^{-1}(W) $, cioè un punto $ x $ in $ X $ tale che $ f(x) \in W $.

Poiché $ f(x) \in W $ e $ W $ è aperto, per ipotesi esiste un intorno $ V_x $ di $ x $ in $ X $ tale che $ f(V_x) \subset W $.

Questo significa che $ V_x \subset f^{-1}(W) $, quindi $ f^{-1}(W) $ contiene un intorno aperto $ V_x $ intorno a $ x $.

Poiché il punto $ x $ era arbitrario, posso concludere che $ f^{-1}(W) $ è aperto in $ X $.

Conclusione

In conclusione, le due definizioni di continuità, quella con gli insiemi aperti e quella con gli intorni, sono equivalenti.

E così via.