Gli spazi connessi per archi (o per cammini)
Uno spazio topologico S è connesso per archi (o per cammini) se presi due punti qualsiasi A e B dello spazio, esiste un cammino continuo che li congiunge senza uscire dallo spazio.
Ad esempio, considero un foglio di carta senza considerare i bordi.
E' un unico corpo ed è un spazio aperto perché non include i confini.
Dati due punti qualsiasi A e B, posso tracciare un cammino con la penna senza mai staccare la penna dal foglio.
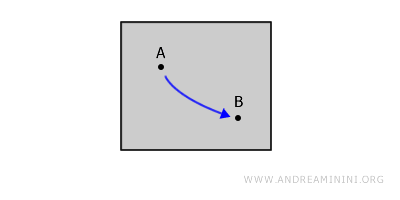
In altre parole, il cammino non esce mai dallo spazio che contiene i due punti A e B.
Uno spazio connesso per archi è anche uno spazio connesso.
Questa affermazione è ovvia, se lo spazio non fosse connesso, sarebbe separato in due parti disgiunte e non tutti i punti dello spazio potrebbero essere collegati tramite un cammino continuo senza uscire dallo spazio.
Tuttavia, non vale sempre il contrario. Uno spazio connesso potrebbe non essere connesso per archi.
Quest'ultimo caso non è semplice da immaginare ma è possibile.
Ad esempio, considero due insiemi Q e T
$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$
$$ T = \{ \ 0 \ \} $$
Nel primo insieme Q ci sono tutti i punti di una sinusoide che è definita per tutti i numeri reali R diversi da zero. Non è definita in zero perché si verificherebbe una divisione per zero ossia un'operazione impossibile.
Nel secondo insieme T c'è solo il punto zero.
I due insiemi Q e T sono infinitamente vicini tra loro. Basta dare un'occhiata al grafico della funzione continua sin(1/x).
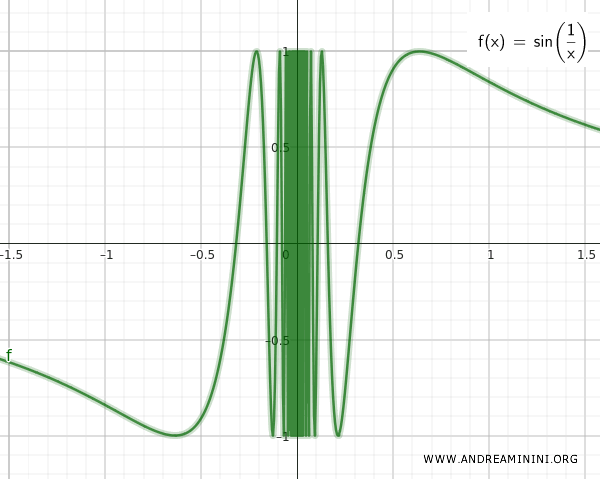
Un insieme S composto dall'unione degli insiemi Q e T.
$$ S = Q \cup T $$
L'insieme S è un insieme connesso perché, essendo Q e T infinitamente vicini, preso un qualsiasi ε>0 esiste un intorno del punto zero (0-ε, 0+ε) che include i punti dell'insieme Q.
Questo accade perché lo zero è un punto di accumulazione della funzione sin(1/x)
Tuttavia, l'insieme S non è un insieme connesso per archi perché non esiste un arco che congiunge un punto qualsiasi di Q con lo zero (insieme T).
Nota. Lo stesso caso non avviene se la funzione è f(x)=1/x perché in questo caso è evidente che l'insieme Q e l'insieme T sono disgiunti, ovvero non sono infinitamente vicini.
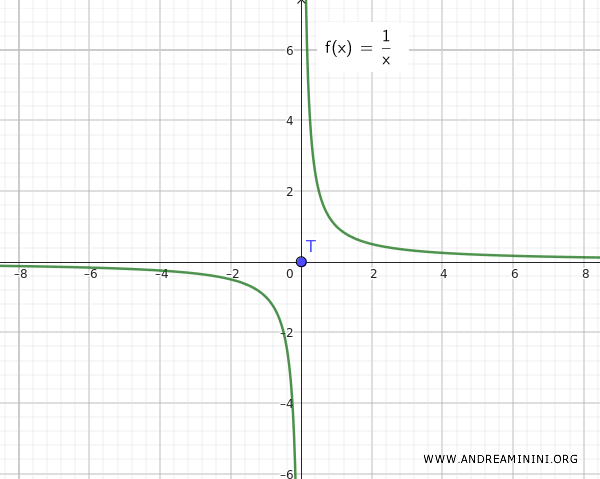
Questo esempio mostra che l'unione di un insieme connesso Q={∀ x ∈ R-{0} , 1/x) e un punto isolato T={0} non necessariamente produce un insieme connesso, a meno che il punto isolato (es. lo zero) non sia anche un punto di accumulazione.
E così via.
