Spazio topologico normale

Uno spazio topologico $ X $ si dice normale se soddisfa due condizioni:

Gli insiemi costituiti da un solo punto sono chiusi
Questo significa che se prendi un qualsiasi punto $ x \in X $, l'insieme $\{x\}$ deve essere chiuso nella topologia data.
Dati due insiemi chiusi e disgiunti, possiamo separarli con insiemi aperti disgiunti
Se $ A $ e $ B $ sono due insiemi chiusi che non si sovrappongono (cioè $ A \cap B = \emptyset $), allora esistono due insiemi aperti $ U $ e $ V $ tali che
- $ A \subset U $
- $ B \subset V $
- $ U $ e $ V $ sono disgiunti, cioè $ U \cap V = \emptyset $.

L'idea è che in uno spazio normale posso sempre "circondare" due insiemi chiusi con regioni aperte che non si toccano, separandoli nettamente.

La normalità garantisce che, se ho due insiemi chiusi separati, posso sempre "allargarli" con insiemi aperti senza che si tocchino.

Questo è importante per la costruzione di funzioni continue che separano i punti.

Un esempio pratico
Note

Un esempio pratico

Considero lo spazio topologico $ X = \mathbb{R} $ con la topologia standard, cioè quella generata dagli intervalli aperti $ (a, b) $.

Ora prendo due insiemi chiusi e disgiunti in $ \mathbb{R} $, ad esempio:

$ A = \{0\} $, cioè un punto singolo.
$ B = [2, 3] $, cioè un intervallo chiuso.

Questi due insiemi sono chiusi nella topologia standard di $ \mathbb{R} $. Inoltre, sono insiemi disgiunti perché non hanno elementi in comune.

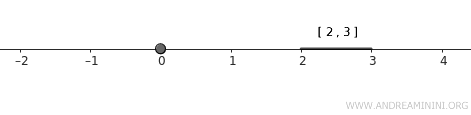
esempio

Nota. L'insieme A contiene un punto singolo e, quindi, non include anche l'intorno del numero. Quindi è chiuso. L'insieme B è un intervallo è un intervallo chiuso, quindi è un insieme chiuso.

Ora voglio trovare due insiemi aperti disgiunti che li contengano.

Ad esempio, posso prendere $ U = (-1, 1) $, un intorno aperto che contiene $ A = \{0\} $.

$$ A \subset U = (-1,1) $$

Poi posso prendere $ V = (1, 4) $, un intorno aperto che contiene $ B = [2,3] $.

$$ B \subset U = (1,4) $$

Questi due insiemi $ U $ e $ V $ sono insiemi disgiunti perché non si sovrappongono ($ U \cap V = \emptyset $).

Questo soddisfa la definizione di spazio normale.

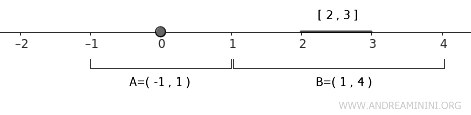
esempio

Lo stesso accade prendendo qualsiasi altra coppia di insiemi chiusi e disgiunti. Posso sempre trovare due insiemi aperti disgiunti che li contengano.

Pertanto, la retta reale $ X = \mathbb{R} $ con la topologia standard è uno spazio normale.

Note

Alcune note aggiuntive sugli spazi topologici normali.

La retta reale $ \mathbb{R} $ con la topologia standard è normale
Non solo soddisfa la condizione di regolarità (cioè è possibile separare un punto e un insieme chiuso con insiemi aperti disgiunti), ma soddisfa anche la condizione più forte di normalità.
Ogni spazio metrico è normale
Se è possibile misurare distanze tra punti con una funzione metrica, lo spazio sarà sempre normale.
Ogni spazio normale è anche regolare
Questo significa che la normalità è una proprietà più forte della regolarità.

E così via.