Il punto fisso in topologia
In topologia un punto fisso di una funzione è un valore che non cambia sotto l'applicazione di quella funzione.
Più formalmente, se ho una funzione f(x), un punto fisso p è tale che f(p)=p. In altre parole, quando p è inserito nella funzione, l'output è lo stesso valore dell'input p.
$$ f(p) = p $$
Ad esempio, ruoto una figura scegliendo come centro il punto interno P.
La rotazione è una funzione che mappa le coordinate dei punti della figura nello spazio.
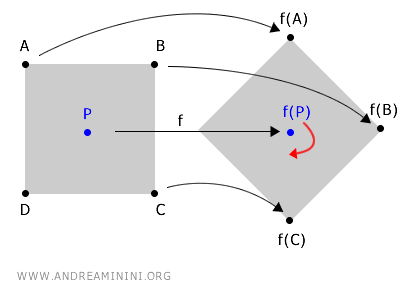
In questo caso il centro della rotazione P è un punto fisso, perché le coordinate del punto centrale P non cambiano con la rotazione f(P).
$$ f(P) \longrightarrow P $$
Il concetto di punto fisso è importante in molti campi della matematica e delle sue applicazioni, come nell'analisi numerica, nella teoria dei giochi e nell'economia.
Un esempio importante nel campo della topologia è il teorema del punto fisso di Brouwer.
Un esempio pratico
Considero la funzione f(x)=sin(x) nell'intervallo chiuso [0, 2π] radianti
$$ f(x) = \sin(x) $$
Un punto fisso di questa funzione è il punto p=0 radianti, perché sin(0)=0.
$$ \sin(0)=0 $$
Il valore in uscita eguaglia il valore in ingresso.
Esempio 2
Considero la funzione f(x)=cos(x) nell'intervallo chiuso [0, 2π] radianti
$$ f(x) = \cos(x) $$
In questo caso x=0 non è un punto fisso perché cos(0)=1 i valori in input e in output differiscono.
Il punto fisso della funzione f(x)=cos(x)f(x)=cos(x) è approssimativamente x=0.73908513
$$ \cos(0.73908513) = (0.73908513 $$
Questo significa che cos(0.73908513) è approssimativamente uguale a 0.73908513.
Il teorema del punto fisso di Brouwer
Questo teorema afferma che:
Per ogni funzione continua che mappa un intervallo chiuso n-dimensionale, esiste almeno un punto fisso.
Si tratta di un teorema di esistenza perché mi dice che esiste "almeno" un punto fisso, ma non mi indica quale è.
Questo teorema ha importanti implicazioni in vari contesti, tra cui la dimostrazione dell'esistenza di stati di equilibrio in sistemi dinamici e nei modelli economici.
E così via.
