Spazio regolare in topologia

In topologia lo spazio regolare è uno spazio topologico che soddisfa una proprietà di separazione più forte della proprietà di Hausdorff.

Se uno spazio è regolare e ha una base numerabile, allora è uno spazio metrizzabile per il teorema di Urysohn.

Qual è la differenza rispetto agli spazi di Hausdorff?

La proprietà degli spazi regolari implica che si possono separare un punto e un insieme chiuso disgiunto tramite insiemi aperti distinti, rafforzando così la nozione di separabilità rispetto agli spazi di Hausdorff che, invece, separano solo coppie di punti distinti mediante insiemi aperti disgiunti.

Nota. Lo spazio regolare si distingue anche dallo spazio normale, perché lo spazio normale è una condizione ancora più forte che richiede che ogni coppia di insiemi chiusi disgiunti possa essere separata da insiemi aperti disgiunti. Questo significa che se uno spazio è normale, allora è automaticamente regolare.  

Va comunque chiarito che la regolarità è un’altra proprietà di separazione e che uno spazio topologico può anche essere regolare senza essere Hausdorff o viceversa. In altre parole esistono spazi di Hausdorff che non sono regolari e spazi regolari che non sono di Hausdorff.

Un esempio pratico

Un esempio pratico di spazio regolare è la retta reale \( \mathbb{R} \) con la topologia standard.

Considero un punto \( x \in \mathbb{R} \) e un insieme chiuso \( C \) che non contiene \( x \).

Ad esempio, prendo il punto \( x=2 \) e lo spazio chiuso \( C \)

\[ C = (-\infty, 0] \cup [5, \infty) \]

Chiaramente, \( x = 2 \notin C \) e \( C \) è chiuso nella topologia standard.

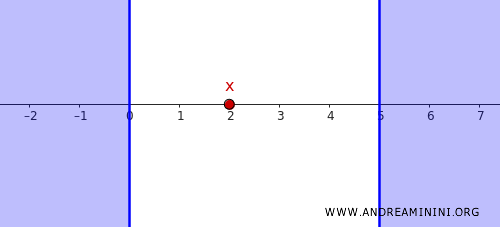
A questo punto devo trovare degli insiemi aperti che separano \( x \) da \( C \)

Il complemento di \( C \)  è un insieme aperto, quindi posso trovare un intervallo aperto contenente \( x \).

Ad esempio, l'insieme \( 0,5 \) contiene il punto \( x=2 \).

\[ (a, b) = (0, 5) \]

Ora scelgo due valori \( c \) e \( d \) tali che contengono il punto \( x = 2 \):

\[ 0 < c < 2 < d < 5 \]

Ad esempio, prendo \( c = 1 \) e \( d = 3 \).

Poi definisco due insiemi aperti:

• \( U = (c, d) = (1,3) \), che contiene il punto \( x = 2 \).
• \( V = (-\infty, c) \cup (d, \infty) = (-\infty, 1) \cup (3, \infty) \), che contiene tutto \( C \).

Questi due insiemi sono disgiunti, cioè \( U \cap V = \emptyset \), quindi soddisfano la condizione di regolarità.

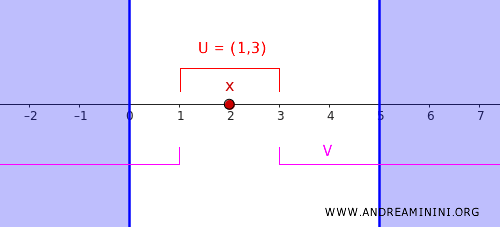
In conclusione, ho separato il punto \( x = 2 \) dall'insieme chiuso \( C \) tramite due insiemi aperti disgiunti \( U \) e \( V \), dimostrando così che la retta reale con la topologia standard è uno spazio regolare.

Note

Alcune osservazioni e note a margine sugli spazi regolari

• Gli assiomi di separazione
  Le proprietà di essere spazi di Hausdorff e di essere regolare rientrano entrambe nella famiglia dei cosiddetti assiomi di separazione, cioè quelle condizioni che definiscono quanto efficacemente uno spazio topologico distingue punti e insiemi mediante aperti disgiunti.

  Nota. In altre parole, dire che uno spazio è Hausdorff significa che due punti distinti possono essere separati da aperti disgiunti. Dire che uno spazio è regolare significa che un punto e un insieme chiuso disgiunto da esso possono essere separati da aperti disgiunti. Entrambe queste proprietà sono quindi tipi di “assiomi di separazione”, perché specificano in che misura la topologia permette di separare elementi dello spazio.

E così via.