Topologia digitale
Una topologia digitale è una struttura topologica definita su uno spazio discreto, come una griglia di punti (pixel in 2D, voxel in 3D), che riflette una proprietà di connessione tra i punti in base a una particolare relazione di adiacenza.
In questo contesto, gli insiemi aperti sono definiti in termini di connessioni tra i punti, e la connessione può variare in base a criteri come la 4-connessione, 8-connessione (in 2D), o la 6-connessione, 18-connessione, 26-connessione (in 3D).
La topologia digitale è utilizzata per analizzare e manipolare strutture discrete in applicazioni come l'elaborazione di immagini, la grafica digitale, e la computer vision, cercando di trasferire concetti della topologia classica a un ambiente discreto.
Insiemi aperti nella topologia digitale
Nella topologia digitale, un insieme \(U\) è considerato aperto se, per ogni punto \(x \in U\), i suoi punti confinanti o vicini secondo il tipo di connessione scelto.
La nozione di "punti confinanti" o "vicini" dipende dalla connessione scelta nello spazio digitale. Per esempio:
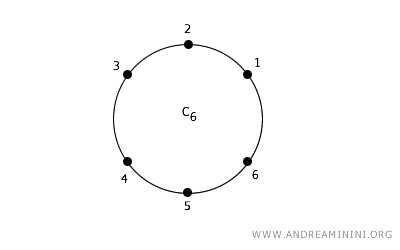
Ad esempio, in un anello o cerchio, ogni punto è confinante ad altri due punti nello spazio discreto. In questo caso si parla di 2-connessione.
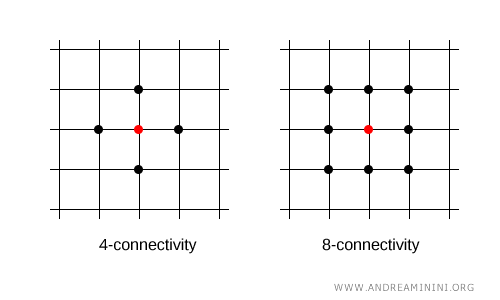
Nel piano (2D), invece, ogni punto può essere connesso ad altri quattro punti (4-connessione) a nord, sud, ovest, est oppure a tutti gli 8 punti adiacenti (8-connessione) includendo anche i punti in diagonale.
Nello spazio digitale a tre dimensioni (3D) la connessione di ogni punto con quelli adiacenti, che appartengono allo spazio digitale e sono anch'essi inclusi in \(U\), potrebbe essere basata sulla 6-connessione, la 18-connessione, o la 26-connessione in 3D) .
Esempio
Considero un insieme di punti su un cerchio digitale (spazio discreto) in una 2-connessione.

Ogni punto dell'insieme ha due punti confinanti adiacenti a destra e a sinistra.
Ad esempio, il punto 2 confina con i punti 1 e 3.
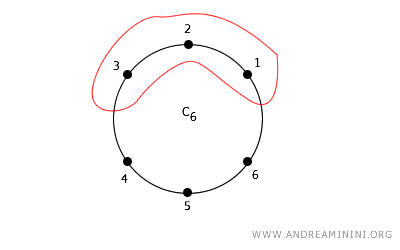
In questo caso, un insieme \( U \) è aperto nella topologia digitale perché tutti i confinanti di ogni punto in \(U\) sono anch'essi contenuti in \(U\).
Questo concetto riflette l'idea di continuità e connessione tra i punti dell'insieme, adattata al contesto discreto degli spazi digitali.
Differenza tra la topologia digitale e la topologia discreta
La topologia digitale non va confusa con la topologia discreta.
Entrambe si basano su uno spazio topologico discreto ma ci sono importanti differenti.
- Topologia discreta
Una topologia su uno spazio \(X\) è detta discreta se ogni possibile sottoinsieme di \(X\) è un insieme aperto. - Topologia digitale
La topologia digitale è una topologia adattata agli insiemi discreti, in cui la definizione di insieme aperto si basa sulla connessione tra i punti:
Qual è la differenza?
Nella topologia discreta tutti i sottoinsiemi sono aperti. Nella topologia digitale, invece, non tutti i sottoinsiemi sono necessariamente aperti. Solo gli insiemi che rispettano il criterio di connessione (basato sulla connessione scelta) sono considerati aperti.
Quindi, la topologia digitale non è una topologia discreta, in quanto non tutti i sottoinsiemi sono necessariamente considerati aperti.
Per esempio, un insieme composto da due pixel isolati non connessi. non è un insieme aperto in una topologia digitale. Lo stesso insieme è, invece, aperto in una topologia discreta.
In altre parole, la topologia digitale è progettata per catturare la nozione di connessione tra i punti in uno spazio digitale.
La topologia discreta, invece, ignora completamente qualsiasi criterio di connessione e tratta ogni punto come un'unità indipendente.
Esempio
Ad esempio, in un insieme di punti \(\{1, 2, 3, 4\}\) in un anello considero una topologia digitale basata sulla 2-connessione.
- L'insieme \(\{1, 2\}\) è aperto nella topologia digitale perché 1 e 2 sono adiacenti.
- L'insieme \(\{1, 3\}\) non è aperto perché 1 e 3 non sono connessi direttamente.
Se considerassi lo stesso insieme di punti \(\{1, 2, 3, 4\}\) nella topologia discreta, sia \(\{1, 2\}\) che \(\{1, 3\}\) sarebbero considerati insiemi aperti, perché in questa topologia tutti i sottoinsiemi sono aperti.
Nota. Nello stesso spazio metrico discreto \(\{1, 2, 3, 4\}\) la topologia digitale si è rivelata più restrittiva rispetto alla topologia discreta, perché impone una struttura di connessione tra i punti per definire gli insiemi aperti.
E così via.
