La topologia del sottospazio
Dato uno spazio topologico \( (X, T) \), dove \( X \) è un insieme e \( T \) è una collezione di insiemi aperti che definiscono la topologia su \( X \). Se \( Y \) è un sottoinsieme di \( X \), la topologia del sottospazio su \( Y \) è data dalla collezione di insiemi \[ T_Y = \{ U \cap Y \mid U \in T \} \] E' anche detta topologia indotta.
In altre parole, un insieme \( V \subseteq Y \) è considerato aperto nella topologia del sottospazio se può essere scritto come l'intersezione di \( Y \) con un insieme aperto \( U \) nello spazio originale \( X \).
Quindi, tutti gli insiemi aperti nella topologia sottospazio $ Y $ sono nella forma \( U \cap Y \), dove \( U \) è aperto in \( X \).
$$ V_{open \ in \ Y} = U \cap Y $$
Allo stesso modo, gli insiemi chiusi nella topologia di sottospazio $ Y $ sono nella forma \( C \cap Y \), dove \( C \) è chiuso in \( X \).
$$ V_{closed \ in \ Y} = C \cap Y $$
Questo significa che un sottospazio topologico è un un sottoinsieme di uno spazio topologico a cui viene assegnata una topologia derivata dalla topologia dello spazio originale.
Nota. Insiemi aperti nel sottospazio topologico $ Y $ potrebbero anche non essere aperti nello spazio topologico $ X $. In generale possono esserci insiemi aperti in Y ma chiusi in X o viceversa, oppure insiemi aperti o chiusi sia in Y che in X. E ovviamente possono anche esserci insiemi clopen, ovvero sia aperti che chiusi. Nel primo esempio di questi appunti mostro un caso simile e spiego perché questo può accadere.
Esempio pratico
Immagino di avere lo spazio topologico \( \mathbb{R} \) con la topologia standard, dove gli insiemi aperti sono gli intervalli aperti.
Sia \( Y = [0, 1] \) un sottoinsieme di $ \mathbb{R} $
La topologia del sottospazio su \( Y \) considera gli insiemi del tipo:
$$ U \cap [0, 1] $$
Dove \( U \) è un insieme aperto in \( \mathbb{R} \).
Ad esempio, l'insieme (-1, 0.5) è aperto nello spazio topologico $ \mathbb{R} $
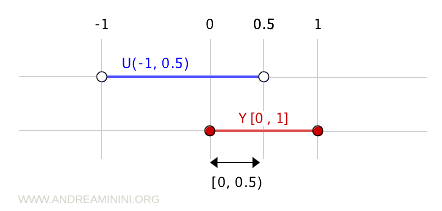
L'intersezione di (-1, 0.5) con l'insieme \( Y = [0, 1] \) è un insieme aperto nel sottospazio topologico in \( Y \).
$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$
Quindi,l'insieme $ [0, 0.5) $ è aperto nel sottospazio \( Y \).
Viceversa, l'insieme $ [0,0.5] $ è chiuso nella topologia di sottospazio $ Y $ perché posso ottenerlo tramite l'intersezione dell'insieme chiuso [-1,0.5] in $ X $ con l'insieme $ Y $
$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$
In sintesi, il sottospazio topologico \( Y \) eredita una struttura topologica dallo spazio originale \( X \) tale che gli insiemi aperti in \( Y \) sono delle intersezioni di \( Y \) con gli insiemi aperti di \( X \).
Nota. Insiemi del tipo [0,a) o (a,1] dove 0<a<1 sono chiusi nella topologia standard in $ \mathbb{R} $ ma sono aperti nel sottospazio topologico perché si possono ottenere come intersezione tra Y=[0,1] e un insieme aperto in $ \mathbb{R} $. Ad esempio, prendo l'insieme aperto (-1;0.5) in $ \mathbb{R} $ e lo interseco con Y=[0,1] $$ (-1;0.5) \cap [0,1] = [0,0.5) $$ L'intervallo [0,0.5) è aperto nel sottospazio Y anche se non è un insieme aperto nella topologia standard in $ \mathbb{R} $.
Nota che ci sono insiemi che sono aperti sia nella topologia di sottospazio $ Y $ e sia in $ X $. Ad esempio, l'insieme (0.2,0.8)
Ci sono insiemi che sono chiusi sia nella topologia $ Y $ che in quella $ X $, come l'insieme [0.2,0.8]
Infine, nella topologia del sottospazio \( Y = [0, 1] \), l'insieme \( [0, 1] \) è sia aperto che chiuso.
- Aperto
Per dimostrare che \( [0, 1] \) è aperto nel sottospazio \( Y \), devo trovare un insieme aperto \( U \) in \( \mathbb{R} \) tale che \( U \cap Y = [0, 1] \). Posso semplicemente prendere \( U = \mathbb{R} \), che è chiaramente aperto in \( \mathbb{R} \). Allora: $$ U \cap Y = \mathbb{R} \cap [0, 1] = [0, 1] $$ Quindi, \( [0, 1] \) è aperto nel sottospazio \( Y \). - Chiuso
Per dimostrare che \( [0, 1] \) è chiuso nel sottospazio \( Y \), devmo trovare un insieme chiuso \( C \) in \( \mathbb{R} \) tale che \( C \cap Y = [0, 1] \). Posso prendere \( C = [0, 1] \), che è chiuso in \( \mathbb{R} \). $$ C \cap Y = [0, 1] \cap [0, 1] = [0, 1] $$ Quindi, \( [0, 1] \) è chiuso nel sottospazio \( Y \).Nota. In alternativa, posso dimostrare che \( [0, 1] \) è chiuso in \( Y \) osservando che il complemento di \( [0, 1] \) in \( Y \) è l'insieme vuoto, che è aperto in qualsiasi topologia. Poiché il complemento di un insieme aperto è chiuso, ne consegue che \( [0, 1] \) è chiuso in \( Y \).
In conclusione, l'insieme \( [0, 1] \) nella topologia del sottospazio \( Y = [0, 1] \) è sia aperto che chiuso.
Questo tipo di insieme viene anche chiamato "insieme clopen", una contrazione dei termini "closed" e "open".
Esempio 2
Considero la topologia standard sull'insieme dei numeri reali \(\mathbb{R}\)
In questa topologia ogni insieme aperto (a,b) con a>b è un insieme aperto.
Un sottospazio topologico di \(\mathbb{R}\) è l'insieme dei numeri interi \(\mathbb{Z}\), perché ogni numero intero posso ottenerlo come intersezione di intervalli aperti dell'insieme dei numeri reali.
Ad esempio, il numero intero 7 posso ottenerlo facendo intersecare l'insieme aperto (6.5,7.5) di \(\mathbb{R}\) con l'insieme dei numeri interi \(\mathbb{Z}\)
$$ (6.5,7.5) \cap \mathbb{Z} = \{ 7 \} $$
Allo stesso modo posso ottenere qualsiasi altro numero intero.
Quindi, ogni numero intero è un insieme aperto nel sottospazio topologico in \(\mathbb{Z}\).
Per la stessa ragione è un insieme aperto nel sottospazio anche ogni sottoinsieme di \(\mathbb{Z}\)
Ad esempio, per ottenere l'insieme {6,7,8} mi basta intersecare l'insieme aperto (5.5,8.5) con l'insieme \(\mathbb{Z}\)
$$ (5.5,8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$
Il sottospazio topologico in \(\mathbb{Z}\) è anche detto topologia discreta.
Nota. La topologia discreta su $ \mathbb{Z} $ non è un sottospazio della topologia standard su $ \mathbb{R} $; piuttosto, è una topologia a sé stante. Tuttavia, la topologia del sottospazio che $ \mathbb{Z} $ eredita dalla topologia standard su $ \mathbb{Z} $ risulta essere equivalente alla topologia discreta su $ \mathbb{Z} $.
Esempio 3
Prendo come esempio lo spazio euclideo tridimensionale \(\mathbb{R}^3\) con la topologia standard dove gli insiemi aperti sono quelli che possono essere scritti come unioni di sfere aperte.
Ora, considero la sfera unitaria \( S^2 \) definita come l'insieme di punti in \(\mathbb{R}^3\) che hanno distanza 1 dall'origine:
$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$
La topologia del sottospazio su \( S^2 \) è definita come segue:
$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ è aperto in } \mathbb{R}^3 \} $$
In altre parole, un insieme \( V \subseteq S^2 \) è aperto nella topologia del sottospazio se e solo se può essere scritto come l'intersezione di \( S^2 \) con un insieme aperto \( U \) in \(\mathbb{R}^3\).
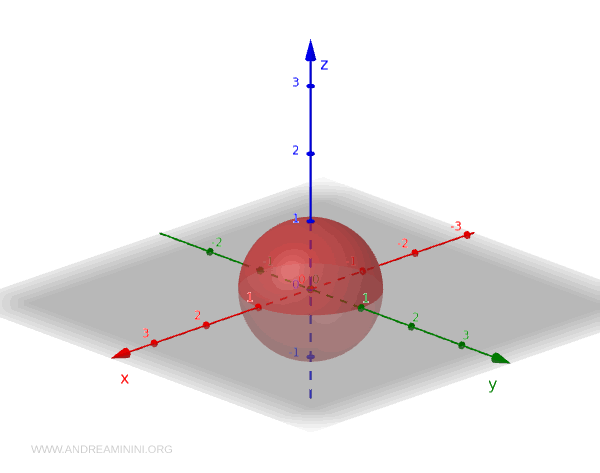
Ecco alcuni esempi di Insiemi Aperti in \( S^2 \)
- Unione di sottospazi aperti in \(\mathbb{R}^3\)
Considero l'insieme aperto \( U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 < 2 \} \). L'intersezione di \( U \) con \( S^2 \) è: $$ U \cap S^2 = S^2 $$ perché ogni punto su \( S^2 \) soddisfa la condizione \( x^2 + y^2 + z^2 = 1 \), che è chiaramente minore di 2. Quindi, \( S^2 \) è aperto in se stesso. - Una piccola porzione della sfera
Considero \( U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \text{ e } z > 0 \} \). Questo \( U \) rappresenta la parte superiore della sfera unitaria (emisfera superiore). L'intersezione con \( S^2 \) è: $$ U \cap S^2 = \{ (x, y, z) \in S^2 \mid z > 0 \} $$ Questo insieme rappresenta la parte superiore della sfera ed è aperto nella topologia del sottospazio \( T_{S^2} \). - Insiemi aperti e chiusura
L'insieme vuoto \( \emptyset \) e \( S^2 \) stesso sono aperti in \( S^2 \).
- L'intersezione finita di insiemi aperti in \( S^2 \) è aperta in \( S^2 \).
- L'unione arbitraria di insiemi aperti in \( S^2 \) è aperta in \( S^2 \).
In sintesi, la sfera \( S^2 \) come sottospazio topologico di \(\mathbb{R}^3\) eredita una struttura topologica dalla topologia standard di \(\mathbb{R}^3\) dove gli insiemi aperti in \( S^2 \) sono intersezioni di \( S^2 \) con insiemi aperti in \(\mathbb{R}^3\).
Le proprietà della topologia del sottospazio
Ecco le principali proprietà della topologia del sottospazio:
- Insiemi aperti
Gli insiemi aperti in \( Y \) sono tutti dell'forma \( U \cap Y \), dove \( U \) è aperto in \( X \). - Insiemi vuoti e completi
L'insieme vuoto \( \emptyset \) e l'insieme \( Y \) stesso sono sempre aperti in \( Y \):
- \( \emptyset \) è aperto perché \( \emptyset = \emptyset \cap Y \).
- \( Y \) è aperto perché \( Y = X \cap Y \). - Intersezioni finite
L'intersezione di un numero finito di insiemi aperti in \( Y \) è ancora aperta in \( Y \). Se \( V_1, \ldots, V_n \) sono aperti in \( Y \), allora: $$ V_1 \cap \cdots \cap V_n = (U_1 \cap Y) \cap \cdots \cap (U_n \cap Y) = (U_1 \cap \cdots \cap U_n) \cap Y $$ Dove ciascun \( U_i \) è aperto in \( X \), e l'intersezione finita di insiemi aperti in \( X \) è aperta in \( X \). - Unioni arbitrari
L'unione arbitraria di insiemi aperti in \( Y \) è ancora aperta in \( Y \). Se \( V_\alpha \) è aperto in \( Y \) per ogni \( \alpha \) in qualche indice \( I \), allora: $$ \bigcup_{\alpha \in I} V_\alpha = \bigcup_{\alpha \in I} (U_\alpha \cap Y) = \left( \bigcup_{\alpha \in I} U_\alpha \right) \cap Y $$ Dove ciascun \( U_\alpha \) è aperto in \( X \), e l'unione arbitraria di insiemi aperti in \( X \) è aperta in \( X \).
Note
Alcune note a margine sui sottospazi
- La topologia standard su qualsiasi sottospazio Y di \(\mathbb{R^n}\) è una topologia equivalente a un sottospazio topologico di \(\mathbb{R^n}\).
Esempio. L'insieme Y=[-1,0)U(0,1] è un sottoinsieme di $ \mathbb{R} $ Nella topologia standard su Y gli intervalli [-1,0) e (0,1] sono entrambi aperti, perché posso ottenerli come intersezione di Y con gli insiemi aperti della topologia standard sui numeri reali $ \mathbb{R} $. Ad esempio, considero gli insiemi aperti (-1.5,0.5) e (0,1.5) della topologia standard in $ \mathbb{R} $ $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ Quindi, la topologia standard su Y è equivalente a un sottospazio topologico della topologia standard su $ \mathbb{R} $. In questo caso gli intervalli [-1,0) e (0,1] sono anche chiusi nella topologia standard su Y, perché il complemento dell'insieme aperto [-1,0) è (0,1], pertanto (0,1] è un insieme chiuso. Allo stesso modo il complemento dell'insieme aperto (0,1] è [-1,0) nella topologia standard su Y, pertanto [-1,0) è un insieme chiuso. In conclusione, gli insiemi [-1,0) e (0,1] sono sia aperti che chiusi (clopen) nella topologia standard su Y.
- Teorema della base della Topologia di sottospazio
Questo teorema stabilisce che se ho una base $ B_X $ per la topologia di uno spazio topologico \(X\) e considero un sottoinsieme \(Y \subset X \), allora la collezione degli insiemi ottenuti intersecando \( B \) con \(Y\) forma una base $ B_Y $ per la topologia sottospazio su \(Y\). $$ B_Y = \{ B \cap Y \ | \ B \in B_X \} $$
E così via.
