Confine di un insieme
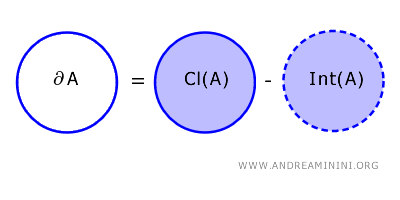
Il confine (o bordo) di un sottoinsieme \( A \) in uno spazio topologico \( X \) è l'insieme dei punti che appartengono alla chiusura di \( A \) ma non al suo interno. \[ \partial A = \text{Cl}(A) - \text{Int}(A) \]
Dove \( \text{Cl}(A) \) è la chiusura di \( A \), cioè l'insieme di tutti i punti di \( A \) insieme ai suoi punti di accumulazione.
Mentre \( \text{Int}(A) \) è l'interno di \( A \), cioè l'insieme di tutti i punti di \( A \) che hanno un intorno completamente contenuto in \( A \).
Anche in questo caso è necessario ribadire che il concetto di confine non è una caratteristica intrinseca dell'insieme ma dipende dalla topologia adottata.
Quindi, il confine di un insieme può cambiare quando si adotta una topologia differente.
In altre parole, il confine di un insieme \( A \) è l'insieme dei punti che sono "vicini" sia all'insieme \( A \) che al suo complemento \( X \setminus A \).
Un esempio pratico
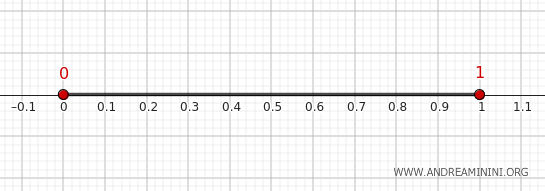
Considero l'insieme \( A = (0, 1) \) come sottoinsieme della retta reale \( \mathbb{R} \) nella topologia standard.
Voglio determinare il confine di \( A \).
1] Calcolo la chiusura di A
La chiusura di \( A \), che indico con \( \text{Cl}(A) \), è l'insieme di tutti i punti di \( A \) insieme ai suoi punti di accumulazione.
Nel caso di \( A = (0, 1) \), la chiusura è l'intervallo chiuso \([0, 1]\), perché ogni punto nell'intervallo \((0, 1)\) è un punto di accumulazione e i punti 0 e 1 sono i limiti dell'intervallo.
$$ \text{Cl}(A) = [0, 1] $$
2] Calcolo l'interno di A
L'interno di \( A \), denotato \( \text{Int}(A) \), è l'insieme di tutti i punti di \( A \) che hanno un intorno completamente contenuto in \( A \).
Nel caso di \( A = (0, 1) \), l'interno è lo stesso insieme \((0, 1)\) perché ogni punto all'interno dell'intervallo aperto ha un intorno completamente contenuto in \( (0, 1) \).
$$ \text{Int}(A) = (0, 1) $$
3] Calcolo il confine di A
Il confine di \( A \) è indicato con \( \partial A \) ed è definito come l'insieme differenza tra la chiusura di \( A \) e l'interno di \( A \):
$$ \partial A = \text{Cl}(A) - \text{Int}(A) $$
Usando i risultati ottenuti nei passi precedenti:
$$ \partial A = [0, 1] - (0, 1) = \{0, 1\} $$
Quindi, nella topologia standard su \( \mathbb{R} \) il confine dell'insieme \( A = (0,1) \) è l'insieme di punti \(\{0, 1\}\).
Questi due punti sono vicini sia all'interno che all'esterno di \( A \) e quindi rappresentano il confine dell'insieme.
Il teorema del confine di un insieme
Un punto \( x \) dello spazio topologico \( X \) appartiene al confine \( x \in \partial A \) di un sottoinsieme \( A \) se e solo se ogni intorno di \( x \) interseca sia \( A \) che \( X - A \).
Secondo questo teorema, posso determinare se un punto \( x \) appartiene al confine di un insieme \( A \) verificando se ogni intorno di \( x \) interseca sia \( A \) che \( X - A \).
Esempio
Considero l'insieme \( A = (0, 1) \) nella retta reale \( \mathbb{R} \) con la topologia standard.
La chiusura e l'interno di questo insieme sono:
$$ \text{Cl}(A) = [0, 1] $$
$$ \text{Int}(A) = (0, 1) $$
Quindi, il confine dell'insieme A è composto solo dai punto 0 e 1.
$$ \partial A = \text{Cl}(A) - \text{Int}(A) = [0, 1] - (0, 1) = \{0, 1\} $$
A questo punto verifico se i punto 0 e 1 appartebgibi al confine usando il teorema precedente.
1] Verifico il punto 0
Ad esempio, considero l'intorno di zero \( (0-\epsilon, 0+\epsilon) \) con \( \epsilon > 0 \).
Questo intorno interseca \( A \) perché ogni intorno di 0 contiene punti che appartengono a \( (0, 1) \).
L'intorno interseca anche \( X - A \), ovvero \( (-\infty, 0] \cup [1, \infty) \), perché contiene punti minori di 0.
Poiché ogni intorno di 0 interseca sia \( A \) che \( X - A \), posso concludere che \( 0 \in \partial A \).
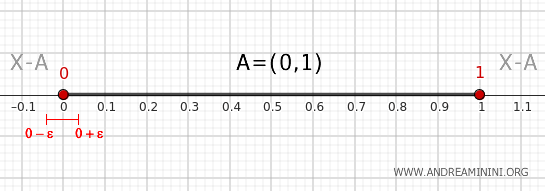
2] Verifico il punto 1
Consideriamo un intorno di 1, ad esempio l'intervallo \( (1-\epsilon, 1+\epsilon) \) con \( \epsilon > 0 \).
Questo intorno interseca \( A \) perché ogni intorno di 1 contiene punti che appartengono a \( (0, 1) \).
L'intorno interseca anche \( X - A \), ovvero \( (-\infty, 0] \cup [1, \infty) \), perché contiene punti maggiori di 1.
Poiché ogni intorno di 1 interseca sia \( A \) che \( X - A \), posso concludere che \( 1 \in \partial A \).
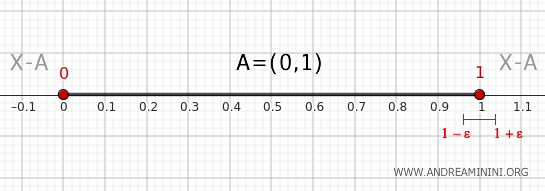
3] Verifico un punto all'interno di (0,1)
Considero un punto qualsiasi all'interno dell'intervallo (0,1).
Ad esempio, l'intervallo \( (0.5-\epsilon, 0.5+\epsilon) \) con \( \epsilon > 0 \).
Questo intorno interseca \( A \) perché ogni intorno di 0.5 contiene punti che appartengono a \( (0, 1) \).
Tuttavia, questo intorno non interseca \( X - A \) poiché tutti i punti di questo intorno appartengono a \( A \).
Poiché esiste un intorno di 0.5 che non interseca \( X - A \), posso concludere che \( 0.5 \notin \partial A \).
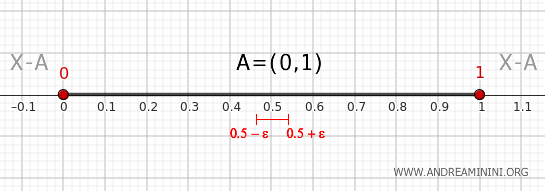
In conclusione, utilizzando il teorema ho verificato che i punti 0 e 1 appartengono al confine di \( A = (0, 1) \), mentre un punto interno come 0.5 non appartiene al confine. Questo conferma che il confine di \( A \) è \(\{0, 1\}\).
Note
Alcune osservazioni e note a margine sui confini degli insiemi
- Il confine \( \partial A \) è un sottoinsieme di \( A \) se e solo se \( A \) è chiuso:
\[ \partial A \subseteq A \Leftrightarrow A \text{ è chiuso} \] - L'intersezione tra il confine e l'insieme A è vuota se e solo se A è aperto
In altre parole, un insieme A è aperto se e solo se nessuno dei suoi punti appartiene al suo confine.
\[ \partial A \cap A = \emptyset \Leftrightarrow A \text{ è aperto} \] - Il confine \( \partial A \) è vuoto se e solo se \( A \) è sia aperto che chiuso (clopen):
\[ \partial A = \emptyset \Leftrightarrow A \text{ è clopen} \] - Il confine \( \partial A \) è l'intersezione tra la chiusura di \( A \) e la chiusura del complemento di \( A \):
\[ \partial A = \text{Cl}(A) \cap \text{Cl}(X - A) \] - I confini \( \partial A \) sono sempre un insieme chiuso
L'intersezione di due insiemi chiusi è sempre un insieme chiuso. E' una proprietà fondamentale negli spazi topologici. Dato che \(\partial A\) è definito come l'intersezione di due insiemi chiusi \(\text{Cl}(A)\) e \(\text{Cl}(X - A)\) \[ \partial A = \text{Cl}(A) \cap \text{Cl}(X - A) \] posso dedurre che \(\partial A\) è sempre chiuso.
- L'intersezione tra il confine \( \partial A \) e l'interno \( \text{Int}(A) \) è vuota:
\[ \partial A \cap \text{Int}(A) = \emptyset \] - L'unione tra il confine \( \partial A \) e l'interno \( \text{Int}(A) \) è uguale alla chiusura di \( A \):
\[ \partial A \cup \text{Int}(A) = \text{Cl}(A) \]
E così via.
