Insieme aperto
Un insieme A è un insieme aperto se per ogni elemento dell'insieme x∈A esiste un intorno che appartiene ancora all'insieme.
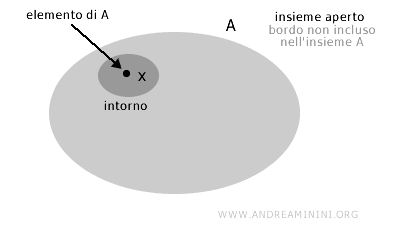
In altre parole, un insieme è detto aperto se, intuitivamente, i suoi "confini" (estremi) non fanno parte dell'insieme.
Più formalmente, un insieme A in uno spazio topologico X si dice aperto se, per ogni punto x di A, esiste un intorno di x completamente contenuto in A.
Nota. Questo significa che intorno a ogni punto dell'insieme, posso trovare una "regione" interamente compresa nell'insieme, senza "toccare" il confine esterno dell'insieme.
Un esempio pratico
Un esempio semplice di un insieme aperto in una linea è un intervallo aperto.
Cos'è un intervallo aperto? Un intervallo aperto su R è definito come l'insieme di tutti i punti x tali che a<x<b dove a e b sono numeri reali con a<b.
Questo intervallo è denotato come (a,b), dove le parentesi tonde indicano che gli estremi a e b non sono inclusi nell'insieme.
Ad esempio, l'intervallo aperto (3,10) è un insieme aperto sulla retta reale.
In questo caso l'insieme A è composto da infiniti numeri tra 3 e 10 esclusi.
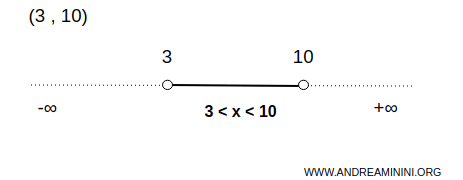
Questo significa che per ogni punto x all'interno di questo intervallo, c'è sempre un piccolo intervallo aperto attorno a x che è completamente contenuto all'interno di (3,10)
Ad esempio, per il punto x=3.1, posso prendere l'intervallo aperto (3.09,3.11) che è interamente contenuto in (3,10).
Lo stesso vale per qualsiasi altro elemento nell'intervallo (3,10), perché tra due numeri reali qualsiasi esistono infiniti altri numeri reali compresi tra questi.
Nota. Anche se considero un numero reale molto piccolo dell'intervallo (3,10), ad esempio 3.001, posso comunque costruire un intorno 3.001±0.00000001 che comprende infiniti numeri reali compresi nell'intorno aperto (3,10).
E' un semplice esempio unidimensionale di insieme aperto.
Altri esempi
Lo stesso esempio posso estenderlo in uno spazio a due dimensioni ossia nel piano.
Ad esempio, l'insieme dei punti di un cerchio con raggio r=1 e centro nell'origine (0;0) degli assi.
$$ x^2+y^2<1 $$
Questa disequazione descrive l'insieme di tutti i punti il cui raggio dal centro (0,0) è minore di 1, quindi NON comprende i punti sulla circonferenza ma solo quelli all'interno del cerchio.
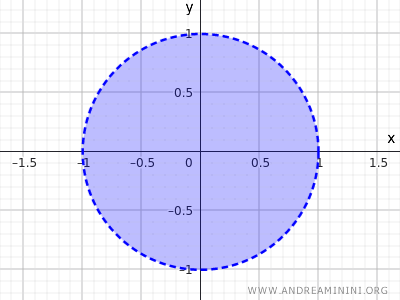
E' un altro esempio di insieme aperto.
Quando un insieme è chiuso?
Per avere un insieme chiuso basta includere i punti della circonferenza nell'insieme.
$$ x^2+y^2 \le 1 $$
In questo caso viene meno la condizione in base alla quale tutti gli elementi dell'insieme hanno un intorno compreso nell'insieme stesso.
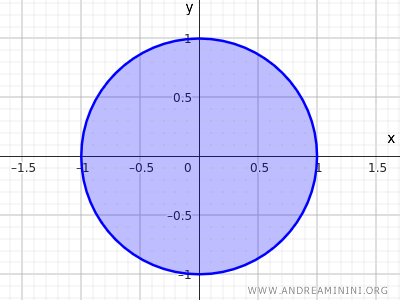
Nel caso dell'insieme chiuso, i punti sulla circonferenza non hanno un intorno interamente compreso nell'insieme.
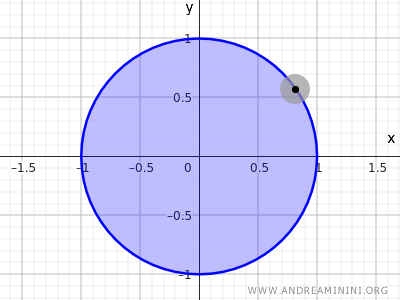
Nota. In topologia l'equazione che definisce il cerchio $ x^2+y^2=1 $ non è né un insieme aperto né chiuso nello spazio euclideo R2, perché considera soltanto i punti sulla circonferenza, senza considerare i punti all'interno. Viceversa, l'insieme dei punti definito dalla disequazione $ x^2+y^2<1 $, che include i punti interni, ma non quelli della circonferenza, è un esempio di insieme aperto. Se considerassi anche i punti della circonferenza $ x^2+y^2\le 1 $ otterrei, invece, un insieme chiuso.
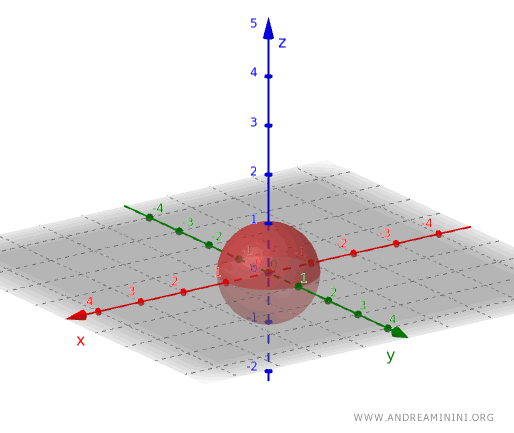
Applicando il medesimo principio, posso creare un insieme aperto nello spazio tridimensionale considerando, per esempio, l'insieme dei punti situati all'interno di una sfera, escludendo però quelli che giacciono sulla sua superficie.
La scelta della topologia
Gli intervalli aperti sono molto utili perché sono intuitivi e danno subito un'idea di cosa sia un insieme aperto.
Tuttavia, il concetto di insieme aperto è molto più astratto e non andrebbe limitato ai soli intervalli aperti.
Pertanto, una volta capito di cosa stiamo parlando è opportuno approfondire meglio il concetto.
Il concetto di insieme "aperto" dipende dalla topologia che scelgo di applicare su uno spazio.
L'idea chiave da capire è che la definizione di insiemi aperti può variare drasticamente a seconda della topologia che si applica a uno spazio.
In alcuni spazi, un insieme che sembra "chiuso" in una topologia standard può essere considerato "aperto" in un'altra topologia.
In altre parole, qualsiasi insieme può essere considerato aperto a seconda della topologia che si definisce per uno spazio.
Cos'è una topologia? Una topologia su uno spazio è essenzialmente una collezione di insiemi considerati "aperti" secondo certe regole che questi insiemi devono soddisfare, come l'unione arbitraria di insiemi aperti che è ancora un insieme aperto e l'intersezione di un numero finito di insiemi aperti che è ancora un insieme aperto.
Per questa ragione è opportuno non limitare il pensiero agli esempi più comuni e intuitivi di insiemi aperti, come intervalli aperti o dischi aperti.
In topologia, la definizione di "insieme aperto" è molto più ampia e può includere insiemi che, a prima vista, non sembrerebbero tali.
Un esempio pratico
Considero lo spazio \( \{a, b\} \) contenente solo due elementi.
Su questo spazio, posso definire almeno due topologie diverse: la topologia banale e la topologia discreta.
- Topologia banale
Nella topologia banale su \( \{a, b\} \), gli unici insiemi aperti sono l'insieme vuoto \( \emptyset \) e lo spazio stesso \( \{a, b\} \). Questa è la topologia più semplice possibile, dove non c'è praticamente nessuna "struttura aperta" al di là dello spazio totale e dell'insieme vuoto. - Topologia discreta
Nella topologia discreta, ogni possibile sottoinsieme di \( \{a, b\} \) è considerato aperto. Questo significa che \( \{a\} \), \( \{b\} \), \( \{a, b\} \), e \( \emptyset \) sono tutti aperti. La topologia discreta è la topologia più "ricca" possibile in termini di insiemi aperti, perché ogni combinazione di punti forma un insieme aperto.
Ora considero l'insieme \( \{a\} \) in entrambe le topologie:
- Nella topologia banale l'insieme {a} non è aperto
L'unico insieme aperto contenente elementi è \( \{a, b\} \), oltre all'insieme vuoto. - Nella topologia discreta l'insieme {a} è aperto
In questa topologia, ogni sottoinsieme di \( \{a, b\} \), inclusi \( \{a\} \) e \( \{b\} \), sono insiemi aperti per definizione.
Pertanto, l'insieme \( \{a\} \) è un insieme aperto sotto la topologia discreta, ma non sotto quella banale.
Questo semplice esempio evidenzia come la definizione di insieme aperto dipenda strettamente dalla topologia scelta.
Teorema degli insiemi aperti
Teorema 1
Dato un insieme aperto X e una topologia T che formano uno spazio topologico (X,T), un sottoinsieme S⊂X è un insieme aperto nello spazio topologico (X,T) se ogni elemento (o punto) s∈S ha un intorno U completamente compreso nel sottoinsieme S ossia U⊂S.
Per definizione S è un insieme aperto perché fa parte dello spazio topologico (X,T).
Quindi, posso vedere il sottoinsieme S come l'intorno di ognuno dei suoi elementi (punti) s∈S.
Da questo deduco che l'intorno di Us di ogni elemento s∈S è a sua volta un insieme aperto compreso in S.
$$ x \in U_s ⊂ S ⊂ X $$
Ogni insieme aperto può essere visto come l'unione di intorni aperti dei suoi punti.
Pertanto, se osservo che ogni elemento (punto) s∈S di un sottoinsieme S ha un intorno Us⊂S compreso in S, posso dedurre che l'insieme S è un insieme aperto aperto perché è l'unione di insiemi aperti.
In altre parole, un insieme è aperto se e solo se, per ogni punto all'interno dell'insieme, esiste un intorno di quel punto che è completamente contenuto nell'insieme.
Esempio. In un tavolo su cui sono sparse delle biglie di vetro. Ogni biglia rappresenta un punto all'interno di un certo insieme. Dire che questo insieme è "aperto" è come dire che attorno a ogni biglia c'è spazio sufficiente per muoversi liberamente senza uscire dal bordo del tavolo. Se per ogni biglia su questo tavolo posso tracciare un cerchio intorno a essa, completamente contenuto sul tavolo (senza toccare i bordi), allora l'insieme di biglie che ho sul tavolo rappresenta un "insieme aperto". In pratica, l'apertura dell'insieme significa che non importa quale biglia scelgo, c'è sempre un po' di spazio "libero" attorno che appartiene ancora all'insieme di biglie sul tavolo.
Teorema 2
Consideriamo un insieme \( X \) e una base \( B \) per una topologia definita su \( X \). Un sottoinsieme \( A \subset X \) si qualifica come insieme aperto rispetto alla topologia generata da \( B \) se, e soltanto se, per ogni elemento \( x \) appartenente ad \( A \), esiste un elemento della base \( B_x \in B \) tale che \( x \) è contenuto in \( B_x \) e \( B_x \) è completamente contenuto in \( A \), cioè \( B_x \subseteq A \).
Questo teorema afferma una proprietà fondamentale delle topologie che vengono generate da una base.
In termini più semplici, ogni punto in un insieme aperto \( A \) deve avere un "piccolo spazio" attorno \( B_x \) che appartiene agli insiemi di base e che sia interamente contenuto in \( A \).
Il che conferma che l'insieme \( A \) è effettivamente aperto nella topologia generata da \( B \).
Dimostrazione. Se A è un insieme aperto nella topologia generata dalla base B sull'insieme X, dove A⊆X, allora A è l'unione degli elementi di base per definizione. Quindi, ogni elemento x di A appartiene almeno a un elemento di base Bx e quest'ultimo è interamente contenuto nell'insieme A, ovvero Bx⊂A, poiché l'insieme A é l'unione degli elementi di base. Di conseguenza vale anche l'inverso. Se ogni elemento x di A è contenuto in almeno un elemento di base Bx che è interamente contenuto in A, ovvero Bx⊂A, allora l'insieme A è aperto nella topologia generata da B.
Esempio
Dato il set \( X = \{1, 2, 3, 4, 5\} \) e la base per una topologia su \( X \) come \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \), provo a determinare se l'insieme \( A = \{1, 2, 3\} \) è un insieme aperto.
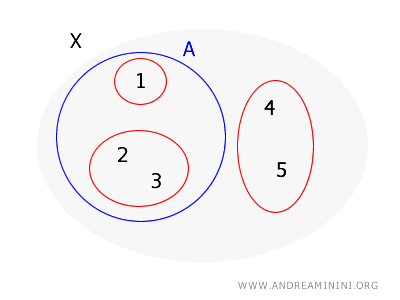
Per ogni punto in \( A \), devo trovare un insieme di base che lo contenga e che sia completamente all'interno di \( A \):
- Per il punto \( 1 \) in \( A \), c'è l'insieme di base \( \{1\} \) che contiene \( 1 \) ed è completamente contenuto in \( A \).
- Per il punto \( 2 \) in \( A \), l'insieme di base \( \{2, 3\} \) contiene \( 2 \) ed è completamente contenuto in \( A \).
- Per il punto \( 3 \) in \( A \), lo stesso insieme di base \( \{2, 3\} \) contiene \( 3 \) ed è interamente contenuto in \( A \).
Ogni punto in \( A \) è contenuto in un insieme di base che è a sua volta contenuto in \( A \), e quindi \( A \) soddisfa la condizione del teorema.
Di conseguenza, posso concludere che \( A \) è un insieme aperto nella topologia generata dalla base \( B \).
Esempio 2
Considero lo stesso insieme \( X = \{1, 2, 3, 4, 5\} \) e la stessa base per una topologia su \( X \) definita come \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \) dell'esempio precedente.
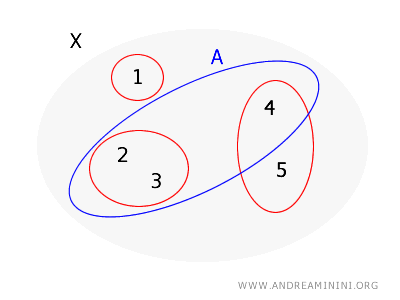
Questa volta, però, voglio verificare se l'insieme \( A = \{2, 3, 4\} \) è un insieme aperto.
- Per il punto \( 2 \), posso usare l'insieme di base \( \{2, 3\} \), che è interamente contenuto in \( A \).
- Per il punto \( 3 \), c'è lo stesso insieme di base \( \{2, 3\} \) lo contiene ed è interamente contenuto in \( A \).
- Per il punto \( 4 \), non c'è un insieme di base che lo contenga e che sia allo stesso tempo completamente all'interno di \( A \) perché l'unico insieme di base che contiene il 4 è \( \{4, 5\} \), che non è completamente all'interno di \( A \) (perché include il 5 che non è in \( A \)).
Quindi, secondo il teorema, l'insieme \( A \) non è un insieme aperto nella topologia generata dalla base \( B \), perché non per ogni punto in \( A \) esiste un insieme di base che è completamente contenuto in \( A \).
E così via.
