Omeomorfismi
Un omeomorfismo è una trasformazione topologica caratterizzata da una funzione biunivoca continua e da una funzione inversa continua.
In pratica, significa che posso trasformare uno spazio in un altro e poi tornare indietro senza "rompere" o "incollare" nulla.
In termini più semplici, un omeomorfismo può essere pensato come un modo di deformare uno spazio in un altro senza "strappare" o "incollare" nulla.
Ad esempio, una tazza con il manico e una ciambella (toro) sono considerate omeomorfe nella topologia, perché posso immaginare di deformare una in forma dell'altra attraverso una serie di trasformazioni continue. E viceversa.

In topologia sono due figure equivalenti perché entrambe hanno un "buco". Il buco della ciambella e il buco del manico della tazzina. Posso appiattire la tazza stirandola intorno al manico, ottenendo così una ciambella.
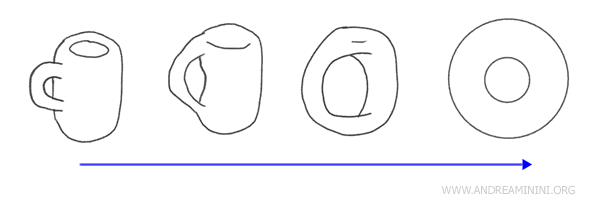
Quando due spazi topologici sono collegati da un omeomorfismo, si dice che sono "spazi omeomorfi", il che implica che, da un punto di vista topologico, sono essenzialmente lo stesso spazio, anche se possono sembrare molto diversi geometricamente.
Le caratteristiche di un omeomorfismo
Ecco le caratteristiche principali di un omeomorfismo:
- Funzione biunivoca
Un omeomorfismo è una funzione che stabilisce una corrispondenza uno-a-uno (biunivoca) tra gli elementi di due spazi topologici. Ogni elemento di un spazio è associato a un unico elemento dell'altro spazio, e viceversa. - Continuità
L'omeomorfismo deve essere una funzione continua. Ciò significa che piccole variazioni nell'input della funzione portano a piccole variazioni nell'output. - Funzione inversa continua
Non solo l'omeomorfismo stesso deve essere continuo, ma anche la sua funzione inversa deve essere continua. In altre parole, la mappatura può essere "invertita" mantenendo la continuità. - Conservazione delle proprietà topologiche
Gli omeomorfismi conservano le proprietà topologiche degli spazi, come la continuità, la connessione e la compattazione. Questo significa che se due punti sono connessi in un modo specifico in uno spazio, lo saranno anche nell'altro spazio dopo la trasformazione.
Pertanto, un omeomorfismo è una funzione continua e invertibile tra due spazi topologici $ X $ e $ Y $, e anche la funzione inversa è continua, che conserva le proprietà topologiche degli spazi.
In pratica, un omeomorfismo è un modo per "deformare" uno spazio in un altro senza romperlo o incollarlo insieme. È una sorta di "corrispondenza perfetta" tra due forme o spazi.
Va ricordato che la definizione di continuità in topologia è la seguente:
Dati due spazi topologici \(X\) e \(Y\), una funzione \(f: X \to Y\) si dice continua se, per ogni insieme aperto \(V\) in \(Y\), la controimmagine \(f^{-1}(V)\) è un insieme aperto in \(X\).
In altre parole, una funzione continua in topologia "mantiene" la struttura degli insiemi aperti quando mappa punti da un insieme all'altro.
Quindi, la continuità in topologia è una versione più flessibile e astratta del concetto di continuità che si trova nell'analisi matematica.
Nota. In analisi matematica la continuità si basa sulla distanza tra i punti. In topologia, invece, la continuità si basa sulla struttura degli insiemi aperti, che è più generale e non richiede una nozione di distanza.
Un esempio pratico
Provo a spiegare il concetto di omeomorfismo e continuità con l'idea di insiemi aperti in modo semplice.
Considero due insiemi spazi topologici $ X = \{a, b, c, d\} $ e $ Y = \{1, 2\} $
- Nello spazio \( X \) gli insiemi aperti sono: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
- Nello spazio \( Y \) gli insiemi aperti sono: \(\{\}, \{1\}, \{1, 2\}\).
Una funzione \( f: X \rightarrow Y \) è continua se, per ogni insieme aperto nello spazio \( Y \), la controimmagine è un insieme aperto in \(X\).
Supponiamo di avere una funzione \( f: X \rightarrow Y \) data da:
\( f(a) = 1 \), \( f(b) = 1 \), \( f(c) = 2 \), \( f(d) = 2 \)
Per semplicità rappresento la funzione $ f $ e i due spazi topologici cerchiando gli insiemi aperti.
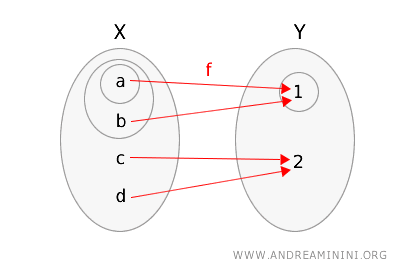
Verifico se soddisfa la definizione di continuità topologica.
- Se prendo l'insieme aperto \(\{1\}\) in \( Y \), la controimmagine in \( X \) è \( f^{-1}(\{1\}) = \{a, b\} \). Questo insieme \(\{a, b\}\) è aperto in \( X \)
- Se prendo l'insieme aperto \(\{1, 2\}\) in \( Y \), la controimmagine è \( f^{-1}(\{1, 2\}) = \{a, b, c, d\} \). Anche questo è un insieme aperto in \( X \).
Poiché ogni controimmagine di un insieme aperto in \( Y \) è aperta in \( X \), questa funzione è continua.
Nota. Ho tralasciato di considerare l'insieme vuoto perché è per definizione aperto in ogni spazio topologico.
Vediamo cosa accade se considero una funzione diversa \( g: X \rightarrow Y \) definita da:
\( g(a) = 1 \), \( g(b) = 1 \), \( g(c) = 1 \), \( g(d) = 2 \)
Anche in questo caso rappresento la funzione $ g $ e i due spazi topologici cerchiando gli insiemi aperti.
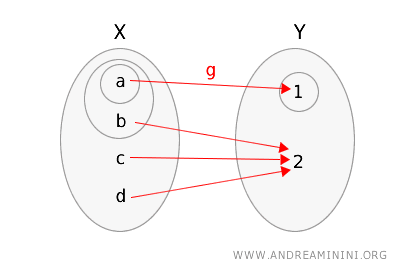
Verifico se soddisfa la definizione di continuità topologica.
- Se prendo l'insieme aperto \(\{1\}\) in \( Y \), la controimmagine in \( X \) è \( g^{-1}(\{1\}) = \{a, b, c\} \). Questo insieme non è aperto in \( X \).
Poiché c'è almeno un insieme aperto in \( Y \) , in questo caso \(\{1\}\)), la cui controimmagine non è aperta in \( X \), la funzione \( g \) non è continua.
Nota. In conclusione, una funzione è continua se, quando prendo qualsiasi insieme aperto nell'insieme di arrivo (\( Y \)), la controimmagine in \( X \) è anche un insieme aperto. In caso contrario, non è continua. Nel primo esempio, la funzione \( f \) è continua perché ogni volta che prendo un insieme aperto in \( Y \), ottengo un insieme aperto in \( X \). La funzione \( g \) non è continua perché questo non accade per tutti gli insiemi aperti.
La definizione di omeomorfismo
Dati due spazi topologici \( X \) e \( Y \) e una funzione biunivoca \( f: X \to Y \) invertibile \( f^{-1}: Y \to X \), se sia \( f \) che \( f^{-1} \) sono funzioni continue, allora \( f \) è detto un omeomorfismo e i due spazi \( X \) e \( Y \) sono detti spazi omeomorfi \( X \cong Y \)
Due spazi omeomorfi sono anche detti topologicamente equivalenti.
Che significa?
Essere omeomorfi o topologicamente equivalenti significa che i due spazi sono "essenzialmente gli stessi" dal punto di vista topologico, anche se potrebbero sembrare diversi come forma geometrica.
Questa definizione conferma tutte le caratteristiche principali di un omeomorfismo:
- Biezione: La funzione \( f: X \to Y \) deve essere una corrispondenza biunivoca, cioè per ogni elemento di \( X \) c'è uno e un solo corrispondente in \( Y \), e viceversa.
- Continuità di \( f \): La funzione \( f \) deve essere continua. Questo significa che, dato un insieme aperto in \( Y \), la sua controimmagine (l'insieme da cui proviene) in \( X \) deve essere aperta.
- Continuità di \( f^{-1} \): Anche l'inversa della funzione \( f \), cioè \( f^{-1}: Y \to X \), deve essere continua. Questo significa che per ogni insieme aperto in \( X \), la sua immagine sotto \( f \) deve essere un insieme aperto in \( Y \).
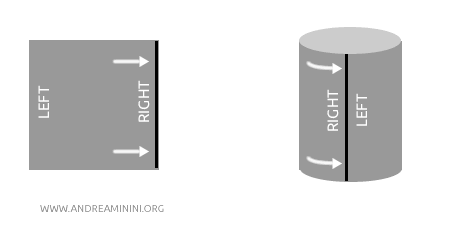
Esempio. Prendo un foglio di carta e lo arrotolo fino a formare un cilindro. Il cilindro e il foglio piatto sono omeomorfi, perché posso "trasformare" il cilindro nel foglio senza strappi o incollature, semplicemente stendendolo e viceversa. La topologia (la struttura degli insiemi aperti) rimane invariata, anche se la forma geometrica cambia.
E' importante sottolineare che la continuità di una biezione \( f \) non implica necessariamente la continuità della sua inversa \( f^{-1} \) a meno che \( f \) non sia anche un'applicazione aperta.
In altre parole, se la funzione $ f $ è continua e biettiva, questo non implica necessariamente che anche la sua inversa \( f^{-1} \) sia continua e il tutto sia un omeomorfismo.
In topologia, una funzione \( f: X \rightarrow Y \) è continua se la controimmagine di ogni insieme aperto in \( Y \) è un insieme aperto in \( X \).
Tuttavia, questo non garantisce che l'immagine di ogni insieme aperto in \( X \) sia aperta in \( Y \).
Perché la funzione inversa \( f^{-1} \) sia continua, \( f \) deve essere non solo continua e biettiva, ma anche un'applicazione aperta (funzione aperta).
Esempio
Considero i due spazi topologici:
- \( X = (a, b) \) con la topologia \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
- \( Y = (1, 2) \) con la topologia \( T_Y = \{\emptyset, Y\} \).
Definisco una funzione \( f: X \to Y \) tale che \( f(a) = 1 \) e \( f(b) = 2 \)
La funzione \( f \) è chiaramente biettiva, poiché ogni elemento di \( X \) ha una corrispondenza unica con un elemento di \( Y \) e viceversa.
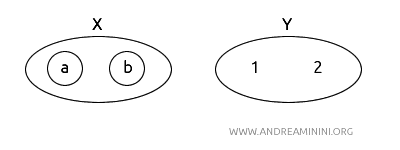
Nota. Nello schema gli insiemi aperti sono i cerchi. Ad esempio, oltre agli insiemi, gli insiemi {a,b}, {a} e {b} sono aperti in X mentre l'insieme {1,2} è aperto in Y. Gli insiemi vuoti sono aperti in ogni topologia per definizione. Per semplicità non li ho rappresentati.
Analizzo ora la continuità di \( f \) e della sua inversa \( f^{-1} \).
- Continuità della funzione \( f \)
Per verificare la continuità di \( f \), devo controllare che la controimmagine di ogni aperto di \( Y \) tramite \( f \) sia un aperto di \( X \). Gli aperti di \( Y \) sono \( \emptyset \) e \( Y \):- \( f^{-1}(\emptyset) = \emptyset \), che è un aperto in \( T_X \)
- \( f^{-1}(Y) = X \), che è un aperto in \( T_X \)
- Continuità dell'inversa \( f^{-1} \)
Ora, consideriamo la funzione inversa \( f^{-1}: Y \to X \), che è definita come \( f^{-1}(1) = a \) e \( f^{-1}(2) = b \)
Per verificare la continuità di \( f^{-1} \), devo controllare che la controimmagine di ogni aperto di \( X \) tramite \( f^{-1} \) sia un aperto di \( Y \). Gli aperti di \( X \) sono \( \emptyset \), \(\{a\}\), \(\{b\}\) e \( X \):- \( f^{-1}(\emptyset) = \emptyset \), che è un aperto in \( T_Y \)
- \( f^{-1}(\{a\}) = \{1\} \), che non è un aperto in \( T_Y \) perché l'unico aperto di \( T_Y \) che contiene \( 1 \) è \( Y \) stesso
- \( f^{-1}(\{b\}) = \{2\} \), che non è un aperto in \( T_Y \) per la stessa ragione
- \( f^{-1}(X) = Y \), che è un aperto in \( T_Y \)
In conclusione, la funzione \( f \) è biettiva e continua, ma la sua inversa \( f^{-1} \) non è continua. Pertanto, $ f $ non è un omeomorfismo.
Questo dimostra che una funzione biettiva e continua non implica necessariamente la continuità della sua inversa.
Nota. In questo esempio, la discontinuità di \( f^{-1} \) è legata alla natura degli aperti in \( X \) e \( Y \): \( X \) ha degli aperti "piccoli" (come \(\{a\}\) e \(\{b\}\)), mentre \( Y \) ha una topologia più grossolana, con solo \( \emptyset \) e \( Y \) come aperti.
Esempio 2
Considero i due spazi topologici:
- \( X = (a, b) \) con la topologia \( T_X = \{\emptyset, \{a\}, X\} \).
- \( Y = (1, 2) \) con la topologia \( T_Y = \{\emptyset, \{1\}, Y\} \).
Definisco una funzione \( f: X \to Y \) tale che \( f(a) = 1 \) e \( f(b) = 2 \)
Anche in questo caso funzione \( f \) è biettiva, perché ogni elemento di \( X \) ha una corrispondenza unica con un elemento di \( Y \) e viceversa.
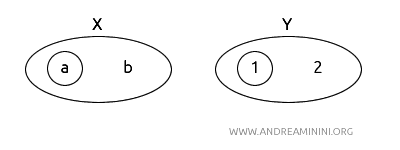
Analizzo la continuità della funzione $ f $ e della sua inversa $ f^{-1} $
- Continuità della funzione \( f \)
Per verificare la continuità di \( f \), dobbiamo controllare che la controimmagine di ogni aperto di \( Y \) tramite \( f \) sia un aperto di \( X \). Gli aperti di \( Y \) sono \( \emptyset \), \(\{1\}\) e \( Y \):
- \( f^{-1}(\emptyset) = \emptyset \), che è un aperto in \( T_X \)
- \( f^{-1}(Y) = X \), che è un aperto in \( T_X \)
- \( f^{-1}(\{1\}) = \{a\} \), che è un aperto in \( T_X \)
- Continuità dell'inversa \( f^{-1} \)
Ora, consideriamo la funzione inversa \( f^{-1}: Y \to X \), che è definita come \( f^{-1}(1) = a \) e \( f^{-1}(2) = b \). Per verificare la continuità di \( f^{-1} \), dobbiamo controllare che la controimmagine di ogni aperto di \( X \) tramite \( f^{-1} \) sia un aperto di \( Y \). Gli aperti di \( X \) sono \( \emptyset \), \(\{a\}\) e \( X \):
- \( f^{-1}(\emptyset) = \emptyset \), che è un aperto in \( T_Y \)
- \( f^{-1}(\{a\}) = \{1\} \), che è un aperto in \( T_Y \)
- \( f^{-1}(X) = Y \), che è un aperto in \( T_Y \)
In questo caso, la funzione \( f \) è biettiva e continua, e anche la sua inversa \( f^{-1} \) è continua. Pertanto, $ f $ è un omeomorfismo.
La differenza rispetto all'esempio precedente risiede nella scelta delle topologie sui due spazi.
Nota. Questo esempio dimostra che con scelte opportune delle topologie su \( X \) e \( Y \), è possibile avere una funzione biettiva e continua con inversa continua, diversamente dall'esempio precedente in cui la continuità dell'inversa non era garantita.
Differenza tra omeomorfismo e trasformazioni topologiche
A volte si parla di omeomorfismi per indicare genericamente le trasformazioni topologiche, perché sono le trasformazioni più frequenti.
In realtà, le trasformazioni topologiche e gli omeomorfismi sono strettamente correlati ma non esattamente la stessa cosa.
- Trasformazioni topologiche
Questo è un termine generale che si riferisce a qualsiasi tipo di trasformazione applicata in un contesto topologico. In pratica, si tratta di una mappatura o una deformazione di uno spazio topologico in un altro che mantiene certe proprietà topologiche, come la connessione e la continuità. Le trasformazioni topologiche includono una varietà di trasformazioni come omeomorfismi, isotopie, omotopie, e diffeomorfismi. - Omeomorfismi
Un omeomorfismo è un tipo specifico di trasformazione topologica. È una trasformazione biunivoca e continua tra due spazi topologici, con una funzione inversa che è anch'essa continua. In termini semplici, un omeomorfismo permette di trasformare uno spazio in un altro e poi di ritorno, senza "rottura" o "colla". Due spazi tra cui esiste un omeomorfismo sono considerati essenzialmente "gli stessi" dal punto di vista topologico, anche se possono apparire molto diversi geometricamente.
Quindi, mentre tutti gli omeomorfismi sono trasformazioni topologiche, non tutte le trasformazioni topologiche sono omeomorfismi.
Alcune trasformazioni topologiche possono avere caratteristiche o restrizioni diverse da quelle degli omeomorfismi.
Note a margine
Alcune osservazioni e note a margine sugli omeomorfismi
- Proprietà tologica
Una proprietà topologica è una caratteristica di uno spazio topologico che rimane invariata quando applico un omeomorfismo. In altre parole, se due spazi topologici sono omeomorfi (cioè c'è una corrispondenza biunivoca e continua tra di loro, con l'inversa che è anche continua), allora condividono le stesse proprietà topologiche. - Teorema di Hausdorff sugli omeomorfismi
Il teorema afferma che se \( f: X \to Y \) è un omeomorfismo e \( X \) è uno spazio di Hausdorff, allora anche \( Y \) sarà uno spazio di Hausdorff. Ciò significa che, poiché un omeomorfismo preserva le proprietà topologiche, lo spazio \( Y \) eredita la proprietà di Hausdorff da \( X \). - L'equivalente di un omeomorfismo in algebra astratta è un isomorfismo tra gruppi. In un isomorfismo tra gruppi la funzione biunivoca preserva la struttura algebrica nelle operazioni del gruppo. In un omeomorfismo, invece, la funzione biunivoca la struttura degli insiemi aperti negli spazi topologici.
E così via.
