Punto di convergenza in uno spazio topologico

In uno spazio topologico $ X $ un punto $ x \in X $ è detto punto di convergenza della successione $ (x_n) $ se, per ogni intorno $ U $ di $ x $, esiste un intero positivo $ N $ tale che per tutti i $ n \geq N $, $ x_n \in U $.

In altre parole, la successione $ (x_n) $ converge a $ x $ se, a partire da un certo indice $ N $, tutti i termini della successione sono contenuti in ogni intorno di $ x $.

Matematicamente, questo si esprime come:

$$ \lim_{n \to \infty} x_n = x \quad $$

In questo caso, $ x $ è chiamato il punto di convergenza o limite della successione $ (x_n) $.

Un esempio pratico

Vediamo un esempio concreto con la successione $ \frac{1}{x_n} $ nello spazio topologico $ X = \mathbb{R} $ con la topologia standard.

$$ x_n = \left( \frac{1}{n} \right) $$

Voglio mostrare che la successione $ \left( \frac{1}{n} \right) $ converge a 0. Ovvero, voglio dimostrare che 0 è il punto di convergenza della successione $ \left( \frac{1}{n} \right) $.

Per farlo, prendo un qualsiasi intorno $ U $ di 0.

Nella topologia standard di $ \mathbb{R} $, un intorno $ U $ di 0 contiene un intervallo aperto del tipo $ (-\epsilon, \epsilon) $ per qualche $ \epsilon > 0 $.

Devo trovare un numero intero positivo $ N $ tale che per ogni $ n \geq N $, $ \frac{1}{n} \in (-\epsilon, \epsilon) $.

Dato un $\epsilon > 0$, posso scegliere $ N = \left\lceil \frac{1}{\epsilon} \right\rceil $. Quindi, per ogni $ n \geq N $, ho:

$$ n \geq \frac{1}{\epsilon} \implies \frac{1}{n} \leq \epsilon. $$

Di conseguenza, $ \left| \frac{1}{n} \right| < \epsilon $ per ogni $ n \geq N $.

Pertanto, per ogni intorno $ U $ di 0, esiste un numero $ N $ tale che per ogni $ n \geq N $, $ \frac{1}{n} \in U $. Questo dimostra che $ \lim_{n \to \infty} \frac{1}{n} = 0 $.

In sintesi, $ 0 $ è il punto di convergenza della successione $ \left( \frac{1}{n} \right) $.

$$ \lim_{n \rightarrow \infty} \frac{1}{n} = 0 $$

In parole povere, la successione $ \frac{1}{n} $ converge a zero perché, a partire da un certo punto, tutti i termini della successione stanno dentro qualsiasi intorno di zero.

Ecco una tabella con i primi dieci valori della successione.

$$
\begin{array}{|c|c|}
\hline
n & \frac{1}{n} \\
\hline
1 & 1 \\
2 & 0.5 \\
3 & 0.333 \\
4 & 0.25 \\
5 & 0.2 \\
6 & 0.167 \\
7 & 0.143 \\
8 & 0.125 \\
9 & 0.111 \\
10 & 0.1 \\
\hline
\end{array}
$$

Se ad esempio prendo $ N=5 $ dove $ x_5= \frac{1}{5} = 0.2 $ per ogni n>5 i punti successivi appartengono allo stesso intorno U=(0 , 0.2).

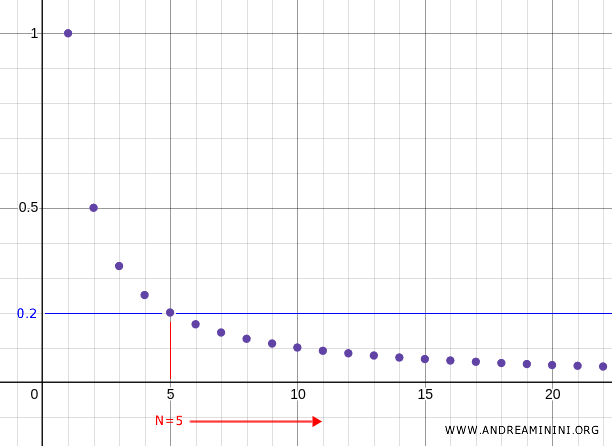
esempio di punto di convergenza

Lo stesso accade se prendo qualsiasi altro valore di N.

Ad esempio, se considero $ N=10 $ dove $ x_10=0.1 $, per ogni $ n>10 $ la successione è compresa nell'intorno U = (0, 0.1) e via dicendo

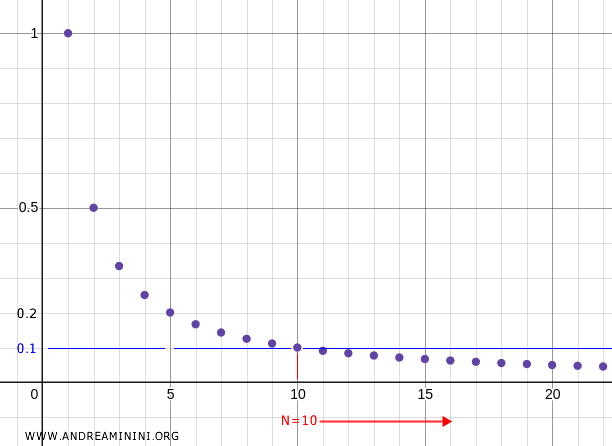
la successione

Quindi, zero è il punto di convergenza della successione di punti.

E così via.