Insieme chiuso
Un insieme B in uno spazio topologico X è detto insieme chiuso se contiene tutti i suoi punti di frontiera e il suo complemento X-B rispetto allo spazio totale è un insieme aperto.
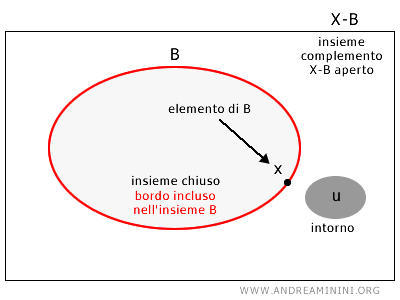
In altre parole, un insieme è chiuso se i suoi "confini" (estremi) sono elementi che appartengono all'insieme stesso.
Più formalmente, un insieme B in uno spazio topologico X si dice chiuso se per ogni elemento dell'insieme complemento u∈X-B esiste un intorno che appartiene ancora all'insieme complemento X-B
Detto in modo più semplice, un insieme è chiuso se il suo complemento è un insieme aperto.
Nota. L'insieme chiuso è un concetto matematico della topologia che si definisce in relazione agli insiemi aperti. Per spiegare questo concetto spesso si utilizzano esempi molto semplici come il caso di un intervallo chiuso [0;1] sulla retta e del relativo intervallo aperto (-∞;0)∪(0;∞).
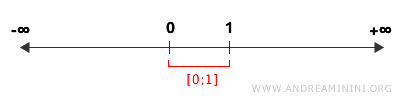
L'intervallo [0, 1], che include i suoi estremi 0 e 1, è un insieme chiuso perché non posso avvicinarmi a un numero fuori da quest'intervallo senza uscire dall'insieme stesso. Inoltre, se prendo il complemento di [0, 1] nell'insieme dei numeri reali, ottengo (-∞, 0) ∪ (1, ∞), che è un insieme aperto. Va però detto che un insieme chiuso non è semplicemente il contrario di un insieme aperto. Nella topologia a volte un insieme può essere sia chiuso che aperto, come l'insieme vuoto o l'intero spazio stesso, e ci sono anche insiemi che non sono né chiusi né aperti.
Un esempio pratico
Considero la retta dei numeri reali R e un qualsiasi intervallo chiuso.
Cos'è un intervallo chiuso? Un intervallo chiuso su R è definito come l'insieme di tutti i punti x tali che a≤x≤b dove a e b sono numeri reali con a<b ed entrambi appartengono all'intervallo.
Gli intervalli chiusi sono rappresentati nella notazione [a,b] , dove le parentesi quadre indicano che gli estremi a e b sono inclusi nell'insieme.
Ad esempio, l'intervallo aperto [3,10] è un insieme chiuso sulla retta dei numeri reali R.
In questo caso l'insieme B è composto da infiniti numeri tra 3 e 10 inclusi.
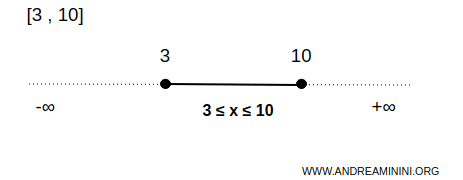
Questo significa che tutti i punti x che soddisfano la condizione 3≤x≤10 sono inclusi nell'insieme, compresi gli estremi 3 e 10.
In questo caso non tutti gli elementi hanno un intorno compreso nell'intervallo [3,10].
Ad esempio, qualsiasi intorno dell'estremo inferiore x=3 non è interamente contenuto nell'intervallo [3,10]
Nota. Se anche considerarssi un intorno infinitesimale, ad esempio 3±0.00000001, questo non sarebbe compreso nell'intervallo chiuso [3.10] perché 3-0.00000001 è minore di 3. Lo stesso vale per l'estremo superiore x=10. Anche in questo caso non esiste un intorno interamente compreso nell'intervallo [3,10]
E' un semplice esempio unidimensionale di insieme chiuso.
Altri esempi di insiemi chiusi
Lo stesso esempio precedente può essere esteso in uno spazio a due dimensioni ossia nel piano.
Ad esempio, l'insieme dei punti di un cerchio con raggio r=1 e centro nell'origine (0;0) degli assi.
$$ x^2+y^2≤1 $$
Questa disequazione descrive l'insieme di tutti i punti il cui raggio dal centro (0,0) è minore o uguale di 1, quindi comprende sia i punti sulla circonferenza e sia quelli all'interno del cerchio.
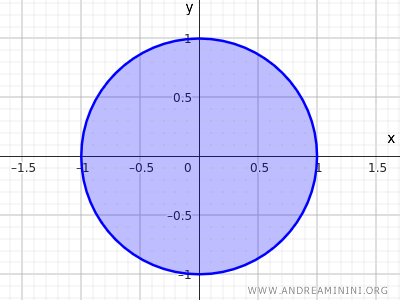
E' un altro esempio di insieme chiuso.
Come si può facilmente intuire, i punti della circonferenza non hanno un intorno interamente incluso nell'insieme.
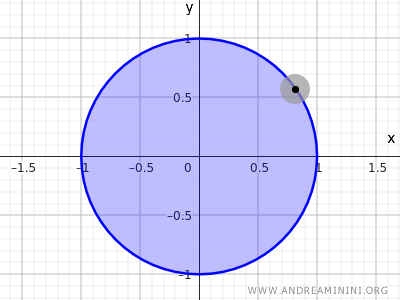
Nota. Nella topologia, il cerchio definito dall'equazione $ x^2+y^2=1 $ non è né un insieme aperto né chiuso nello spazio euclideo R2, poiché considera solamente i punti sulla circonferenza, escludendo l'interno. Viceversa, l'insieme dei punti definito dalla disequazione $ x^2+y^2≤1 $, che include sia i punti interni sia quelli sulla circonferenza, è un esempio di insieme chiuso, perché include tutti i suoi punti di confine (la circonferenza).
Con la stessa logica posso estendere il concetto di insieme chiuso nello spazio a tre dimensioni, tramite la sfera, e nello spazio n-dimensionale con la sfera a n dimensioni.
Il complemento di un insieme chiuso
Il complemento di un insieme chiuso C nello spazio X è un insieme aperto X-C.
Se un insieme C è chiuso, allora il suo complemento X-C nello spazio X è un insieme aperto.
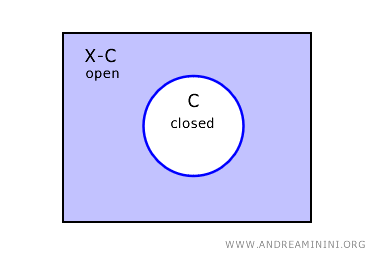
Viceversa, se un insieme U è aperto, allora il suo complemento X-C nello spazio X è un insieme chiuso.
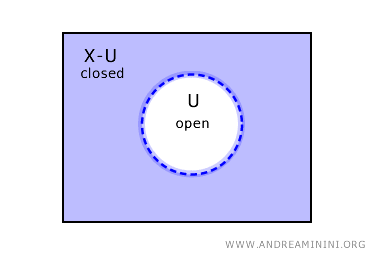
Tuttavia, questi non sono i soli casi possibili. In topologia possono esistere anche insiemi che sono sia chiusi che aperti e insiemi né aperti, né chiusi.
In altre parole, un insieme non chiuso non è detto che sia aperto e un insieme non aperto non è detto che sia chiuso.
Esempio
Ad esempio, considero la topologia T nell'insieme X={a,b,c,d} composto da quattro elementi.
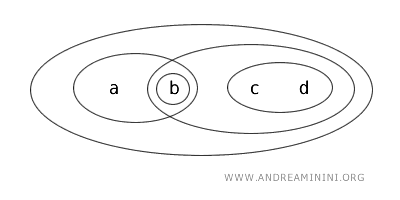
Secondo la topologia T i seguenti insiemi sono "aperti": {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, Ø,
Ora andiamo ad analizzare i vari insiemi nel dettaglio.
- {b} è un insieme aperto. E' definito come "aperto" dalla topologia stessa.
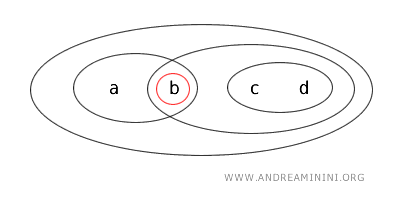
- {a} è un insieme chiuso perché è il complemento di un insieme aperto X-{b,c,d}={a}. Dove X={a,b,c,d}.
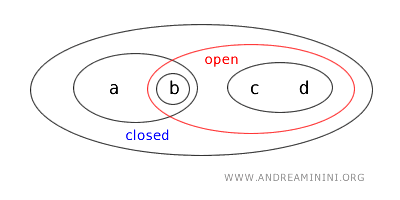
- {a, b} è sia aperto che chiuso, noto anche come "clopen". E' piuttosto insolito nelle topologie comuni su R, ma può accadere in spazi topologici generali. Questo può accadere quando la collezione di insiemi aperti definiti nella topologia include sia l'insieme che il suo complemento. In questo caso, {a,b} è un insieme aperto perché è definito nella topologia T come "aperto".
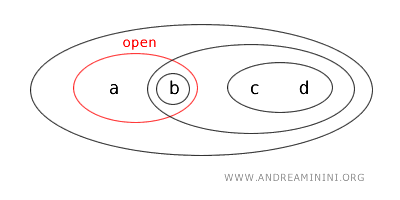
L'insieme {a,b} è anche un insieme "chiuso" perché è il complemento dell'insieme aperto X-{c,d}. Quindi, è contemporaneamente sia aperto che chiuso.
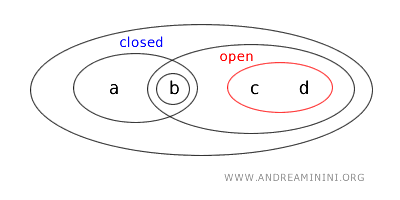
- {b, c} non è né aperto né chiuso, perché non soddisfa le condizioni per essere aperto e non è nemmeno il complemento di un insieme aperto. Non è definito come "aperto" dalla topologia. Inoltre, non è chiuso perché non è il complemento di un insieme aperto. Quindi, l'insieme {b,c} non è né aperto, né chiuso.
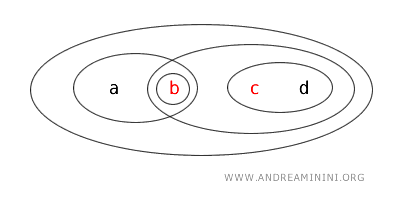
Questo esempio dimostra che in una topologia un insieme può essere aperto, chiuso, sia aperto che chiuso, né aperto e né chiuso.
Le proprietà di un insieme chiuso
Un insieme chiuso è il complemento di un insieme aperto, quindi soddisfa le seguenti proprietà:
- L'insieme vuoto (simbolo Ø) e lo spazio stesso (X) sono sempre considerati chiusi.
- Se prendo l'intersezione (cioè i punti in comune) di insiemi chiusi, il risultato è ancora un insieme chiuso.
- Se unisco un numero finito di insiemi chiusi, il risultato è ancora un insieme chiuso.
Esempio
Ad esempio, nella topologia standard dello spazio euclideo Rn ogni singolo punto è un insieme chiuso.
Per un singolo punto n di una retta (R1), il complemento è l'insieme di tutti i punti su R1 che non sono n.
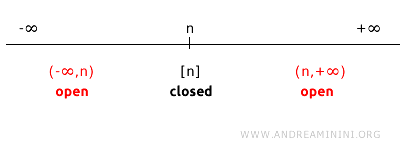
Quindi, il complemento di {n} è l'unione di due intervalli aperti: (−∞,n)∪(n,+∞).
Poiché questi due intervalli (−∞,n) e (n,+∞) sono aperti nella topologia standard, la loro unione (−∞,n)∪(n,+∞) è anche un insieme aperto.
E poiché il complemento di {n} è un insieme aperto, deduco che {n} è un insieme chiuso.
Va però precisato che non è detto ogni singolo punto sia un sempre insieme chiuso, poiché ci sono spazi topologici dove questo non è vero. Una topologia diversa su R (la linea dei numeri reali) potrebbe non avere i punti singoli come insiemi chiusi. Ad esempio, considero una topologia particolare su R che viene generata usando come base gli intervalli aperti (n, n + 1) per ogni numero intero n. In questo tipo di spazio topologico, i punti singoli (n) non sono chiusi perché non includono i "limiti" intorno a loro.
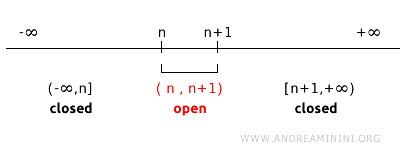
Ad esempio, in questa topologia gli insiemi (1,2) e (2.3) sono insiemi aperti. il complemento dell'insieme aperto (1,2) è l'insieme (-∞,1]∪ [2,+∞), mentre il complemento dell'insieme aperto (2,3) è l'insieme (-∞,2]∪ [3,+∞). Quindi, non si posso trovare un complemento uguale all'insieme chiuso [2]. In generale, in questa topologia, dato un qualsiasi insieme aperto (n,n+1), il suo complemento è l'unione degli insiemi chiusi (-∞,n]∪ [n+1,+∞). Quindi, il complemento di un insieme aperto (n,n+1) non potrà mai essere uguale all'insieme [n]. Pertanto, i singoli punti n in questa topologia non sono considerati insiemi chiusi. Questo dimostra che, anche per i singoli punti di una retta, la definizione di insieme chiuso dipende dalla topologia che si sceglie.
Osservazioni
Alcune osservazioni e note a margine
- Gli insiemi chiusi includono al loro interno tutti i loro punti di accumulazione
Un punto di accumulazione in un insieme è un punto tale che ogni intorno (qualunque piccola regione aperta) di quel punto contiene almeno un altro punto dell'insieme. Quindi, se un insieme è chiuso, include tutti i suoi punti di accumulazione, mentre un insieme aperto potrebbe non farlo.Esempio. Considero l'intervallo chiuso [0, 1] sull'asse reale. Questo intervallo include tutti i suoi punti di accumulazione. Se prendo un qualsiasi punto all'interno dell'intervallo [0, 1], ad esempio 0.5, esiste un interno aperto che contiene infiniti altri punti dell'intervallo [0, 1]. Quindi, 0.5 è un punto di accumulazione.
![esempio 0.5 come punto di accumulazione nell'intervallo chiuso [0,1]](/data/andreamininiorg/punto-di-accumulazione-insieme-chiuso-am-2024-1.gif)
Lo stesso vale per ogni punto dell'intervallo [0, 1] compresi gli estremi zero e uno. Ad esempio, l'estremo inferiore dell'intervallo [0, 1], che è 0, è un punto di accumulazione dell'intervallo perché contiene ancora punti dell'intervallo come 0.1, 0.01, 0.001, ecc.
![gli estremi dell'intervallo chiuso [0,1] sono punti di accumulazione](/data/andreamininiorg/punto-di-accumulazione-insieme-chiuso-am-2024-2.gif)
In conclusione, ogni punto dell'intervallo chiuso [0,1] ha intorni aperti che contengono altri punti dell'intervallo. - L'insieme A è chiuso se e solo se A = Cl(A)
Un insieme \( A \) in uno spazio topologico è un insieme chiuso se coincide con la sua chiusura, cioè \( A = \text{Cl}(A) \). Questo perché la chiusura di \( A \), \( \text{Cl}(A) \), include tutti i punti di \( A \) e tutti i suoi punti di accumulazione. Per definizione, se l'insieme \( A \) contiene tutti i suoi punti di accumulazione, allora è un insieme chiuso.
E così via.
