Punto di accumulazione in topologia

Un punto $x$ in uno spazio topologico $X$ è un punto di accumulazione (o punto limite) di un sottoinsieme $A \subseteq X$ se ogni intorno di $x$ interseca $A$ in un punto diverso da $x$.

Questo significa che in ogni intorno di $x$ c'è almeno un punto di $A$ che non è $x$ stesso.

In altre parole, un punto x è un punto di accumulazione se l'intersezione tra ogni intorno U di x e il sottoinsieme A non è vuota.

$$ U \cap A \not = \emptyset $$

Dove un punto di accumulazione può essere un punto qualsiasi che non necessariamente deve appartenere all'insieme A.

In genere, il concetto di punto di accumulazione è intuitivo in uno spazio topologico reale $\mathbb{R}$. Su una linea, un punto $x$ è un punto di accumulazione di un sottoinsieme $A$ se qualsiasi intorno di $x$, ovvero un intervallo $(x-\epsilon, x+\epsilon)$, contiene punti di $A$ diversi da $x$ stesso.
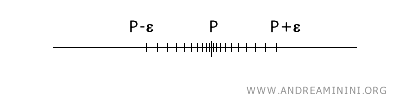
esempio di punto di accumulazione in una linea di numeri reali
La definizione topologica di punto di accumulazione estende questo concetto a uno spazio a n dimensioni $\mathbb{R}^n$, dove un punto $x$ è un punto di accumulazione di $A$ se ogni intorno di $x$ interseca $A$ in un punto diverso da $x$. Questa definizione generale non sempre è altrettanto intuitiva come nel caso di una dimensione.

Esempi pratici
Osservazioni

Esempi pratici

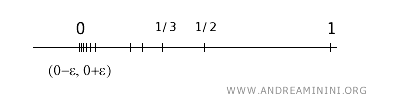
Considero l'insieme $ A $ come un sottoinsieme di $\mathbb{R}$ con la topologia standard.

$$ A = \left\{ \frac{1}{n} \mid n \in \mathbb{N}^+ \right\} $$

Questo insieme contiene i punti $ \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots $, ossia $\{1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots \}$.

Per determinare se $0$ è un punto di accumulazione di $A$, considero qualsiasi intorno aperto $U$ di $0$.

Un tale intorno $U$ conterrà un intervallo aperto $(a, b)$ con $a < 0 < b$.

Dato che $\frac{1}{n}$ tende a $0$ quando $n$ tende all'infinito, posso sempre trovare un punto $\frac{1}{n}$ che appartiene all'intervallo $(a, b)$, per ogni $n$ sufficientemente grande.

Pertanto, ogni intorno di $0$ interseca $A$ in almeno un punto diverso da $0$.

Quindi, secondo la definizione, $0$ è un punto di accumulazione dell'insieme $A$.

esempio di punto di accumulazione

Esempio 2

Considero l'insieme $ B $ come un sottoinsieme di $\mathbb{R}$ nella topologia standard.

$$ B = \left\{ n + \frac{1}{n} \mid n \in \mathbb{N}^+ \right\} $$

Questo insieme contiene i punti $ 1 + 1, 2 + \frac{1}{2}, 3 + \frac{1}{3}, \ldots $, ossia $\{2, 2.5, 3.333\ldots, \ldots \}$.

Esamino il punto $1$.

Ogni intorno aperto $U$ di $1$ conterrà un intervallo aperto $(a, b)$ con $a < 1 < b$.

Tuttavia, tutti i punti di $B$ sono maggiori di $1$ e, per ogni punto $n + \frac{1}{n} \in B$, l'intervallo $(a, b)$ conterrà un punto di $B$ solo se $a < n + \frac{1}{n} < b$.

Dato che non esistono punti di $B$ inferiori a $1$, non è possibile trovare punti di $B$ negli intervalli aperti che contengono $1$.

Quindi, $1$ non è un punto di accumulazione dell'insieme $B$.

Esempio 2

Considero l'insieme $(0, 1] $ come un sottoinsieme di $\mathbb{R}$ con la topologia standard.

Devo determinare i punti di accumulazione di $(0, 1]$.

Secondo la definizione, un punto $x$ è un punto di accumulazione di $(0, 1]$ se ogni intorno di $x$ interseca $(0, 1]$ in un punto diverso da $x$.

Punti all'interno di (0,1]
Per ogni $x \in (0, 1]$, qualsiasi intorno di $x$ sarà un intervallo aperto $(a, b)$ con $a < x < b$. Dato che $x$ è un punto all'interno dell'intervallo $(0, 1]$, ogni intorno di $x$ intersecherà $(0, 1)$ in un punto diverso da $x$. Pertanto, ogni punto $x \in (0, 1]$ è un punto di accumulazione di $(0, 1]$.
Punti agli estremi di (0,1]
Esamino i punti $0$ e $1$.
- Punto $0$: Qualsiasi intorno di $0$ conterrà un intervallo aperto $(a, b)$ con $a < 0 < b$. Anche se $0$ non appartiene a $(0, 1]$, qualsiasi intervallo di questo tipo conterrà infiniti punti di $(0, 1]$. Ad esempio, ogni numero reale positivo molto piccolo sarà in $(0, 1]$). Pertanto, $0$ è un punto di accumulazione di $(0, 1]$.

- Punto $1$: Qualsiasi intorno di $1$ conterrà un intervallo aperto $(a, b)$ con $a < 1 < b$. In questo caso $1$ appartiene a $(0, 1]$ ed è un punto di accumulazione perché qualsiasi intervallo di questo tipo conterrà infiniti punti di $(0, 1]$. Ad esempio, ogni numero reale appena inferiore a $1$ sarà in $(0, 1]$. Pertanto, $1$ è un punto di accumulazione di $(0, 1]$.
Punti fuori da [0, 1]
Per completezza considero un generico punto esterno all'interno e ai punti di accumulazione appena trovati, ossia $x \notin [0, 1]$. Se $x < 0$ o $x > 1$, posso sempre trovare un intorno di $x$ che è completamente disgiunto da $(0, 1]$.
Ad esempio, se $x < 0$, posso prendere un intervallo $(x - \epsilon, x + \epsilon)$ con $\epsilon$ sufficientemente piccolo in modo che non intersechi $(0, 1]$. Analogamente, se $x > 1$, posso trovare un intervallo attorno a $x$ che non intersechi $(0, 1]$. Quindi, nessun punto fuori da $[0, 1]$ è un punto di accumulazione di $(0, 1]$.

In conclusione, i punti di accumulazione dell'insieme $(0, 1)$ nello spazio topologico $\mathbb{R}$ con la topologia standard sono tutti i punti nell'intervallo chiuso $[0, 1]$.

Esempio 4

Devo determinare l'insieme dei punti limite di $ A = (0, 1] $ nella topologia del limite inferiore su $ \mathbb{R} $.

La topologia del limite inferiore su $ \mathbb{R} $ è generata dagli intervalli della forma $[a, b)$ con $ a < b $. Quindi, gli insiemi aperti in questa topologia sono le unioni arbitrarie degli intervalli [a,b).

Un punto $ x $ è un punto limite di un insieme $ A $ se ogni intorno di $ x $ contiene almeno un punto di $ A $ diverso da $ x $.

Analizzo i vari punti dello spazio:

Punti x ∈ (0, 1)
Qualsiasi intorno $[x, x + \epsilon)$ con x in (0,1) contiene punti di A. Quindi, tutti i punti nell'intervallo (0,1) sono punti di accumulazione di A.
Punto x = 1
Qualsiasi intorno $[1 - \epsilon, 1)$ contiene punti di A. Quindi, il punto 1 è un altro punto di accumulazione di A.
Punto x = 0
Qualsiasi intorno $[0, 0 + \epsilon)$ con $\epsilon > 0$ contiene punti di A, quindi anche il punto 0 è un punto limite di A.
Punti x < 0 o x > 1
Qui niente da dire, non ci sono intorni [x,x+ε) che intersecano A. Pertanto, non sono punti di accumulazione di A.

In conclusione, i punti di accumulazione di $ A = (0, 1] $ nella topologia del limite inferiore su $ \mathbb{R} $ sono tutti i punti in $[0, 1]$.

Quindi, l'insieme dei punti limite di $ A $ è $[0, 1]$.

Osservazioni

Alcune osservazioni e note a margine sui punti di accumulazione

Teorema della chiusura di un insieme
La chiusura di un sottoinsieme $A$ in uno spazio topologico $X$ è l'unione di $A$ con l'insieme $A' $ dei suoi punti di accumulazione $$ \text{Cl}(A) = A \cup A' $$ In altre parole, la chiusura $\text{Cl}(A)$ contiene tutti i punti dell'insieme $A$ e tutti i punti di accumulazione di $A$.
Una sequenza di punti converge verso il punto di accumulazione
Se $ A $ è un sottoinsieme dello spazio topologico $ X = \mathbb{R} $ nella topologia standard e il punto $ x $ è un punto accumulazione di $ A $, allora esiste una successione di punti $ x_i \in X $ che converge a $ x $ Nota. il punto limite potrebbe anche non appartenere al sottoinsieme A.
Unicità del punto limite
Nella topologia standard se una sequenza di punti converge a un punto limite $ x $, allora questo è unico. Tuttavia, questo non è detto in generale perché dipende dalla topologia che viene adottata.

E così via.