La continuità di una funzione di inclusione in topologia

Se $ X $ è uno spazio topologico e $ Y $ è un sottoinsieme di $ X $, la funzione di inclusione $ f : Y \to X $ è definita come $ f(y) = y $ per ogni $ y \in Y $ ed è una funzione continua.

Una funzione di inclusione è una funzione che mappa da un sottoinsieme $ Y $ al suo spazio contenitore più grande $ X $.

In altre parole, la funzione di inclusione $ f $ collega ogni elemento di $ Y $ nel corrispondente elemento di $ X $.

Si tratta di una funzione continua in topologia.

Nota. La funzione di inclusione non va confusa con la funzione identità, non sono esattamente la stessa cosa, anche se a volte possono sembrare simili. La funzione di inclusione è una funzione che mappa da un sottoinsieme al suo spazio contenitore più grande, mentre la funzione identità mappa ogni elemento del proprio spazio su sé stesso.

Perché è continua?

In topologia una funzione è continua se per ogni insieme aperto $ U $ in $ X $, la controimmagine di $ U $ attraverso $ f $, cioè $ f^{-1}(U) $, è aperta in $ Y $.

Per la definizione della topologia di sottospazio, gli insiemi aperti di $ Y $ sono esattamente le intersezioni degli insiemi aperti di $ X $ con $ Y $.

$$ f^{-1}(U) = U \cap Y $$

Dato che $ f^{-1}(U) = U \cap Y $ è sempre aperto in $ Y $ se $ U $ è aperto in $ X $, la funzione $ f $ è continua per definizione.

Nota. Questo riflette la proprietà che la topologia di sottospazio su $ Y $ è progettata per rendere la funzione di inclusione continua.

Un esempio pratico

Considero lo spazio topologico $ X = \mathbb{R} $ (la retta dei numeri reali) e il suo sottoinsieme $ Y = (0, 1) $, l'intervallo aperto tra 0 e 1.

La funzione di inclusione $ f : Y \to X $ è definita da $ f(y) = y $ per ogni $ y \in Y $.

$$ f(y) = y \ \ \ \text{per ogni} \ \ y \in (0,1) $$

In altre parole, la funzione $ f $ "inserisce" i punti di $ Y $ che sono i numeri nell'intervallo aperto $ (0, 1) $ all'interno dello spazio $ X $ che è tutta la retta reale $ \mathbb{R} $.

Nella topologia del sottospazio per ogni insieme aperto $ U $ in $ X $, l'intersezione $ U \cap Y $ è un insieme aperto in $ Y $.

Ad esempio, considero l'intervallo aperto $ U = (-1, 0.5) \subset \mathbb{R} $ nella topologia standard su $ X $.

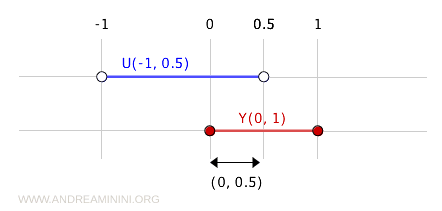
esempio

L'intersezione di questo insieme aperto con $ Y = (0, 1) $ è:

$$ U \cap Y = (-1, 0.5) \cap (0, 1) = (0, 0.5) $$

Quest'ultimo è un intervallo aperto nell'insieme $ Y = (0, 1) $.

Quindi, $ U \cap Y = (0, 0.5) $ è aperto nella topologia di sottospazio su $ Y $.

Poiché per ogni insieme aperto $ U $ in $ X $, l'intersezione $ U \cap Y $ è un insieme aperto in $ Y $, la funzione di inclusione $ f : Y \to X $ è continua.

E così via.