La topologia del prodotto di spazi topologici

Dati due spazi topologici $ X $ e $ Y $, la topologia del prodotto su $X \times Y$ è definita come la topologia generata dalla base $B$ costituita dal prodotto cartesiano di tutti gli insiemi aperti nella forma $U \times V$, dove $U$ è aperto in $X$ e $V$ è aperto in $Y$. $$ B = \{ U \times V \mid U \text{ è aperto in } X \text{ e } V \text{ è aperto in } Y \} $$

L'idea iniziale per creare una topologia su $X \times Y$ è prendere insiemi della forma $U \times V$, dove $U$ è un insieme aperto in $X$ e $V$ è un insieme aperto in $Y$.

Questa collezione di insiemi è indicata con $B$ e forma una base di una topologia.

Dove una base per una topologia è una collezione di insiemi aperti tali che ogni altro insieme aperto dello spazio topologico $X \times Y$ può essere scritto come un'unione di questi insiemi di base.

Quindi, nella topologia prodotto, il prodotto cartesiano di insiemi aperti è ancora un insieme aperto.

Nota. Gli insiemi aperti nella topologia prodotto non sono solo i prodotti cartesiani $X \times Y$ degli insiemi aperti di $X$ e $Y$, ma includono anche tutte le loro possibili unioni. Per questo motivo, la collezione $B$ non è considerata una topologia completa, ma una base per la topologia prodotto. Se si trattasse $B$ come una topologia vera e propria, non comprenderebbe tutti gli insiemi aperti ottenibili tramite l'unione dei prodotti cartesiani.

Lo stesso vale per gli insiemi chiusi.

Nella topologia prodotto, il prodotto cartesiano di insiemi chiusi sono ancora un insieme chiuso.

Anche in questo caso non tutti gli insiemi chiusi della topologia di prodotto sono espressi dal prodotto di insieme chiusi.

In altre parole, come accade per gli insiemi aperti, nella topologia di prodotto possono esistere insiemi chiusi che non sono ottenuti dal prodotto cartesiano di insiemi chiusi.

Un esempio pratico
Il prodotto di più spazi topologici
La base della topologia di prodotto
Note

Un esempio pratico

Faccio un esempio concreto per chiarire il concetto di topologia del prodotto.

Suppongo di avere due spazi topologici semplici:

$ X $ è la retta reale $\mathbb{R}$ con la topologia standard (insiemi aperti sono intervalli aperti $(a, b)$).
$ Y $ è anche la retta reale $\mathbb{R}$ con la stessa topologia standard.

Ora, considero il prodotto $ X \times Y $ che genera il piano cartesiano $ \mathbb{R} \times \mathbb{R} = \mathbb{R}^2$.

Per costruire la base $B$ della topologia del prodotto su $X \times Y$, prendo tutti i prodotti $U \times V$ dove $U$ è un insieme aperto in $X$ e $V$ è un insieme aperto in $Y$.

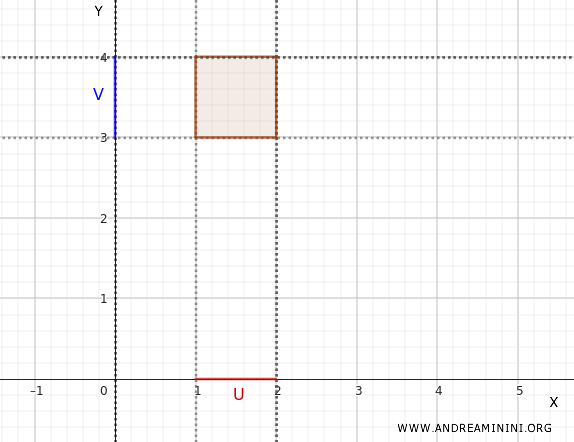
Ad esempio, prendo $U = (1, 2) \subset X$ ovvero un intervallo aperto in $X$

Poi prendo $V = (3, 4) \subset Y$ , un intervallo aperto in $Y$

Allora $U \times V = (1, 2) \times (3, 4)$ è un insieme aperto in $\mathbb{R}^2$. Questo insieme è un rettangolo aperto nel piano cartesiano $\mathbb{R}^2$.

esempio

Vediamo cosa succede con l'unione di due insiemi di base.

Considero $U_1 \times V_1 = (1, 2) \times (3, 4)$

Poi considero $U_2 \times V_2 = (1.5, 2.5) \times (3.5, 4.5)$

Questi insiemi rappresentano due rettangoli aperti nel piano.

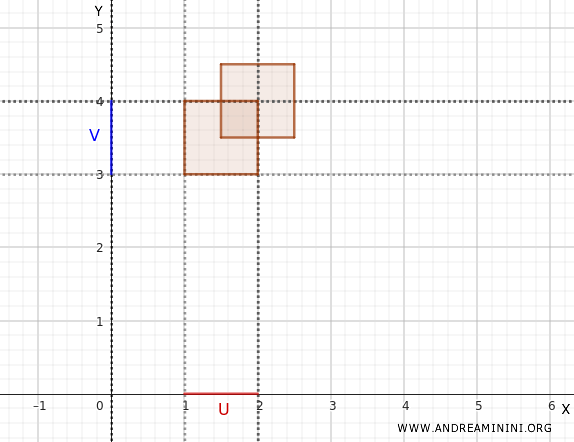
un esempio di unione di insiemi aperti

La loro unione non è nella forma tipica del prodotto cartesiano $U \times V$, ma è comunque un'unione di insiemi di base e, pertanto, rappresenta un insieme aperto della topologia di prodotto:

$$ (1, 2) \times (3, 4) \cup (1.5, 2.5) \times (3.5, 4.5) $$

In questo modo, ogni punto nel piano può essere coperto da un'unione di insiemi di base $U \times V$.

Ad esempio, supponiamo di voler verificare se un punto $(1.8, 3.8)$ è coperto da questa base.

Il prodotto $ (1, 2) \times (3, 4) $ contiene il punto $(1.8, 3.8)$. Quindi, $(1.8, 3.8)$ appartiene all'unione degli insiemi della base.

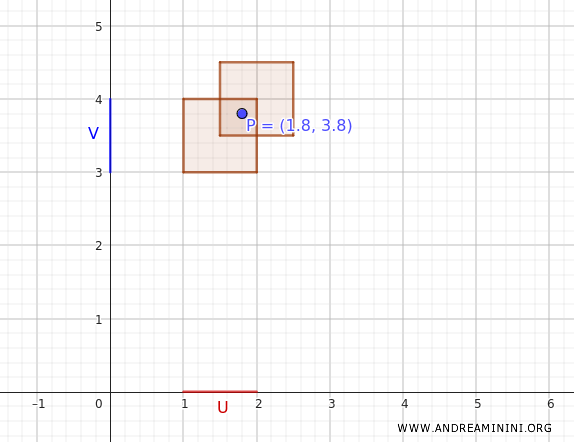
esempio

Questo esempio conferma che la base $B$ genera una topologia valida sul prodotto cartesiano $X \times Y$ degli spazi topologici.

Nota. Questa topologia è chiamata "topologia del prodotto" ed è particolarmente utile perché preserva la struttura aperta degli spazi originari $X$ e $Y$ nel prodotto $X \times Y$.

Esempio 2

Considero due spazi topologici

$X = \{a, b, c\}$ con la topologia $\{\emptyset, \{a\}, \{b, c\}, X\}$
$Y = \{1, 2\}$ con la topologia $\{\emptyset, \{1\}, Y\}$

Per calcolare la topologia prodotto su $X \times Y$, devo prendere tutti i prodotti cartesiani degli insiemi aperti nelle topologie di $X$ e $Y$ e poi considerare tutte le possibili unioni di questi prodotti.

$$ B = \{ U \times V \mid U \text{ è aperto in } X \text{ e } V \text{ è aperto in } Y \} $$

Gli insiemi aperti di $X$ sono:

$\emptyset$
$\{a\}$
$\{b, c\}$
$X = \{a, b, c\}$

Gli insiemi aperti di $Y$ sono:

$\emptyset$
$\{1\}$
$Y = \{1, 2\}$

Ora, calcolo i prodotti cartesiani di questi insiemi:

$\emptyset \times \emptyset = \emptyset$
$\emptyset \times \{1\} = \emptyset$
$\emptyset \times Y = \emptyset$
$\{a\} \times \emptyset = \emptyset$
$\{a\} \times \{1\} = \{(a, 1)\}$
$\{a\} \times Y = \{(a, 1), (a, 2)\}$
$\{b, c\} \times \emptyset = \emptyset$
$\{b, c\} \times \{1\} = \{(b, 1), (c, 1)\}$
$\{b, c\} \times Y = \{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$X \times \emptyset = \emptyset$
$X \times \{1\} = \{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$

Nota. Il prodotto cartesiano tra insiemi è definito come l'insieme delle coppie ordinate i cui primi elementi appartengono al primo insieme e i cui secondi elementi appartengono al secondo insieme. Formalmente, il prodotto cartesiano $A \times B$ è definito come: \[ A \times B = \{(a, b) \mid a \in A \text{ e } b \in B\} \] Ora, se uno dei due insiemi è l'insieme vuoto ($\emptyset$), non ci sono elementi in questo insieme da combinare con gli elementi dell'altro insieme. Di conseguenza, non ci possono essere coppie ordinate in cui almeno un elemento provenga dall'insieme vuoto. Quindi, il prodotto cartesiano di $\emptyset$ con qualsiasi insieme $B$ è l'insieme vuoto. \[ \emptyset \times B = \{(a, b) \mid a \in \emptyset \text{ e } b \in B\} = \emptyset \] In altre parole, non esistono elementi $a \in \emptyset$, quindi non possono esserci coppie $(a, b)$ con $b \in B$. Ad esempio,
\[ \emptyset \times \{1\} = \emptyset \] Questo è il motivo per cui il prodotto cartesiano dell'insieme vuoto con qualsiasi insieme è l'insieme vuoto.

La topologia prodotto è l'insieme di tutte le possibili unioni di questi prodotti cartesiani. Pertanto, la topologia prodotto su $X \times Y$ include:

$\emptyset$
$\{(a, 1)\}$
$\{(a, 1), (a, 2)\}$
$\{(b, 1), (c, 1)\}$
$\{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$\{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$
Qualsiasi altra unione di questi insiemi
Ad esempio, $\{(a, 1)\} \cup \{(b, 1), (c, 1)\} = \{(a, 1), (b, 1), (c, 1)\}$, ecc.

La topologia prodotto su $X \times Y$ è quindi costituita da tutte queste unioni.

Questo conferma che nella topologia prodotto gli insiemi aperti non sono soltanto i prodotti degli insiemi aperti $X \times Y$, in quanto sono aperti anche gli insiemi ottenuti dall'unione dei prodotti cartesiani.

Ad esempio, questa unione di insiemi è un insieme aperto nella topologia prodotto $\{(a, 1)\} \cup \{(b, 1), (c, 1)\} = \{(a, 1), (b, 1), (c, 1)\}$ Quindi, è un errore pensare che solo i prodotti $X \times Y$ siano insiemi aperti nella topologia prodotto.

La base $ B $ della topologia $X \times Y$ è invece formata solo dai prodotti cartesiani non vuoti.

$\{(a, 1)\}$
$\{(a, 1), (a, 2)\}$
$\{(b, 1), (c, 1)\}$
$\{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$\{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$

Il prodotto di più spazi topologici

Lo stesso concetto può essere esteso anche al prodotto di più spazi topologici.

Dati n spazi topologici $ X_1 $, $ X_2 $, fino a $ X_n $, se $ U_i $ è una collezione di insiemi aperti di ciascuno degli spazi $ X_i $, allora la collezione di tutti i prodotti di questi insiemi aperti $ U_1 \times U_2 \times \cdots \times U_n $ forma una base per una nuova topologia sul prodotto degli spazi $ X_1 \times \cdots \times X_n $. $$ B = \{ U_1 \times U_2 \times \cdots \times U_n \mid U_i \text{ è aperto in } X_i \text{ per ogni } i \} $$

La base della topologia di prodotto

In generale, il prodotto cartesiano degli insiemi aperti di due spazi topologici genera una valida base della topologia di prodotto.

$$ B = \{ U \times V \mid U \text{ è aperto in } X \text{ e } V \text{ è aperto in } Y \} $$

Tuttavia, questa base potrebbe essere molto grande all'atto pratico.

Esiste un modo alternativo per ottenere una base della topologia di prodotto più piccola ed efficiente.

Dati due spazi topologici $ X $ e $ Y $, con basi $ B_X $ per la topologia su $ X $ e $ B_Y $ per la topologia su $ Y $, la base della topologia di prodotto su $ X \times Y $ è data dal prodotto cartesiano delle due basi $$ B = \{ U \times V \mid U \in B_X \text{ e } V \in B_Y \} $$

Questo insieme $ B $ è una base per la topologia prodotto su $ X \times Y $.

In altre parole, gli elementi di $ B $ sono gli insiemi base della topologia prodotto, e ogni aperto della topologia prodotto può essere scritto come un'unione di tali prodotti cartesiani $ U \times V $.

Nota. In generale questo concetto posso estenderlo anche al prodotto di più spazi topologici. Dati n spazi topologici $ X_1 , X_2 , ... , X_n $. se $ B_i $ è una base per ciascun spazio $ X_i $, allora i prodotti di questi insiemi formano una base per la topologia prodotto su $ X_1 \times X_2 \times \cdots \times X_n $. $$ B = \{ B_1 \times \cdots \times B_n \ \ \mid \ \ B_i \text{ è una base di } X_i \text{ per } i = 1, \ldots, n \} $$

Esempio

Considero due spazi topologici.

Lo spazio topologico $ X = \{a, b\} $ con la topologia $ \mathcal{T}_X = \{\emptyset, \{a\}, \{b\}, \{a, b\}\} $ ha come base minima $ B_X = \{\{a\}, \{b\}\} $.
Lo spazio topologico $ Y = \{1, 2\} $ con la topologia $ \mathcal{T}_Y = \{\emptyset, \{1\}, \{2\}, \{1, 2\}\} $ ha una base minima $ B_Y = \{\{1\}, \{2\}\} $.

Posso costruire una base minima della topologia prodotto prendendo solo i prodotti cartesiani degli elementi delle basi $ B_X $ e $ B_Y $ anziché tutti gli insiemi aperti di ciascun spazi topologico

$$ B_X = \{\{a\}, \{b\}\} $$

$$ B_Y = \{\{1\}, \{2\}\} $$

Il prodotto cartesiano delle due basi è il seguente:

$$ \{a\} \times \{1\} = \{(a, 1)\} $$

$$ \{a\} \times \{2\} = \{(a, 2)\} $$

$$ \{b\} \times \{1\} = \{(b, 1)\} $$

$$ \{b\} \times \{2\} = \{(b, 2)\} $$

Quindi, la base minima della topologia prodotto su $ X \times Y $ è:

$$ B_{\text{minima}} = \{\{(a, 1)\}, \{(a, 2)\}, \{(b, 1)\}, \{(b, 2)\}\} $$

Questa base minima è sufficiente per generare l'intera topologia prodotto su $ X \times Y $.

Ogni aperto nella topologia prodotto può essere espresso come un'unione di questi insiemi base minimi.

In altre parole, utilizzando solo i prodotti cartesiani degli insiemi atomici (ossia quelli non decomposti ulteriormente), ottengo una base della topologia prodotto che è più piccola ma ancora sufficiente per descrivere la topologia intera.

Dimostrazione

Voglio dimostrare che l'insieme$ B $ è una base per la topologia prodotto su $ X \times Y $

$$ B = \{U \times V \mid U \in B_X \text{ e } V \in B_Y\} $$

Qui, $ B_X $ è una base per la topologia di $ X $ e $ B_Y $ è una base per la topologia di $ Y $.

Nella topologia prodotto, gli insiemi aperti sono unioni di insiemi della forma $ U \times V $, dove $ U $ è un aperto in $ X $ e $ V $ è un aperto in $ Y $.

Per dimostrare che $ B $ è una base per questa topologia, devmo verificare che ogni aperto $ W $ in $ X \times Y $ può essere scritto come unione di elementi di $ B $.

Verifica della proprietà della base

Supponiamo che $ W $ sia un insieme aperto nella topologia prodotto su $ X \times Y $ e che $ (x, y) $ sia un punto in $ W $.

Per la definizione di topologia prodotto, esistono insiemi aperti $ U' \subseteq X $ e $ V' \subseteq Y $ tali che:

$$ (x, y) \in U' \times V' \subseteq W $$

Poiché $ U' $ è aperto in $ X $ e $ B_X $ è una base per la topologia di $ X $, esiste un elemento $ U \in B_X $ tale che:

$$ x \in U \subseteq U' $$

Analogamente, poiché $ V' $ è aperto in $ Y $ e $ B_Y $ è una base per la topologia di $ Y $, esiste un elemento $ V \in B_Y $ tale che:

$$ y \in V \subseteq V' $$

Di conseguenza, posso scrivere:

$$ (x, y) \in U \times V \subseteq U' \times V' \subseteq W $$

Quindi, per ogni punto $ (x, y) \in W $, esiste un elemento $ U \times V $ in $ B $ tale che $ (x, y) $ appartiene a $ U \times V $ e $ U \times V $ è contenuto in $ W $.

Conclusione

Poiché ogni punto $ (x, y) $ in un aperto $ W $ della topologia prodotto appartiene a un elemento della base $ B $ che è contenuto in $ W $, ne consegue che $ B $ copre tutti gli aperti della topologia prodotto.

Pertanto, l'insieme $ B = \{U \times V \mid U \in B_X \text{ e } V \in B_Y\} $ è una base per la topologia prodotto su $ X \times Y $.

E questo conclude la dimostrazione.

Note

Alcune note a margine sulla topologia del prodotto

Teorema del sottospazio del prodotto
Il teorema afferma che se prendo due sottospazi $A$ e $B$ di spazi topologici $X$ e $Y$, la topologia sul loro prodotto $A \times B$ considerato come sottospazio di $X \times Y$ è la stessa della topologia prodotto su $A \times B$, costruita a partire dalle topologie di $A$ e $B$. In sostanza, indipendentemente da come si costruisce la topologia su $A \times B$, si ottiene la stessa struttura topologica. $$ \quad \tau_{A \times B}^{\text{sub}} = \tau_A^{\text{sub}} \times \tau_B^{\text{sub}} $$
Equivalenza topologica del prodotto
Dati tre spazi $ X $, $ Y $, e $ Z $, allora i prodotti $ (X \times Y) \times Z $, $ X \times (Y \times Z) $, e $ X \times Y \times Z $ sono topologicamente equivalenti. In pratica, non importa come li raggruppi, il risultato finale è lo stesso spazio topologico. $$ (X \times Y) \times Z \cong X \times (Y \times Z) \cong X \times Y \times Z $$
Teorema dell'interno del prodotto cartesiano
Due insiemi $A$ e $B$ che appartengono rispettivamente ai spazi topologici $X$ e $Y$, l'interno del prodotto cartesiano $A \times B$ è uguale al prodotto degli interni di $A$ e $B$. $$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$

E così via.