Grafo topologico
Un grafo topologico è uno spazio topologico costruito prendendo un insieme finito di punti, chiamati 'vertici', e un insieme finito di intervalli chiusi mutuamente disgiunti in \(\mathbb{R}\), chiamati 'spigoli', incollati ai vertici secondo una certa regola.
La topologia di questo spazio è determinata dalle identificazioni fatte durante l'incollamento, rendendo il grafo topologico una rappresentazione sia geometrica che topologica di una rete di connessioni tra vertici.
Questo crea un nuovo spazio che ha la struttura di un grafo.
Nota. Si tratta di un tipo di topologia quoziente perché è una topologia applicata a uno spazio per crearne un altro spazio "indotto". Il nuovo spazio viene costruito incollando un insieme di intervalli su un insieme di vertici. In altre parole, prendo degli spazi semplici (come gli intervalli chiusi) e li modifico incollandoli a certi punti per ottenere uno spazio topologico più complesso.
Come costruire un grafo topologico
Un grafo topologico è una costruzione matematica che si ottiene in due passaggi principali:
- Vertici: Si parte con un insieme finito di punti chiamati vertici. Ad esempio, i vertici sono i punti indicati con A, B, C, D, E, F.
- Spigoli: Si considera poi un insieme di intervalli (linee), ognuno con due estremi. Gli estremi di questi intervalli vengono "incollati" (o collegati) a specifici vertici, creando delle connessioni. Queste connessioni (o intervalli) sono chiamate spigoli.
In sostanza, prendo delle linee (intervalli) e le attacco a dei punti (vertici), creando una struttura chiamata grafo.
Questo grafo viene detto "topologico" perché deriva da una costruzione che riguarda il modo in cui gli spazi vengono incollati o attaccati insieme.
Un esempio pratico
Considero 3 intervalli chiusi distinti in \(\mathbb{R}\):
$$ I_1 = [0, 1], \quad I_2 = [0, 1], \quad I_3 = [0, 1] $$
Questi sono semplici segmenti di linea, ognuno con estremi \(0\) e \(1\).
Definisco un insieme $ G $ composto da 3 vertici, che chiameremo \(A\), \(B\) e \(C\).
$$ G = \{ A,B,C \} $$
I vertici sono semplicemente dei punti a cui posso incollare gli estremi degli intervalli.
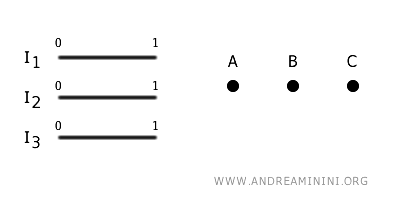
A questo punto, applico l'operazione della topologia quoziente incollando gli estremi degli intervalli a certi vertici.
- Incollo l'estremo \(0\) dell'intervallo \(I_1\) al vertice \(A\) e l'estremo \(1\) di \(I_1\) al vertice \(B\).
- Incollo l'estremo \(0\) dell'intervallo \(I_2\) al vertice \(B\) e l'estremo \(1\) di \(I_2\) al vertice \(C\).
- Incollo l'estremo \(0\) dell'intervallo \(I_3\) al vertice \(A\) e l'estremo \(1\) di \(I_3\) al vertice \(C\).
Il risultato è un grafo con 3 vertici \(A\), \(B\) e \(C\) e 3 spigoli $ (A,B) $, $(B,C) $, $(A,C) $.
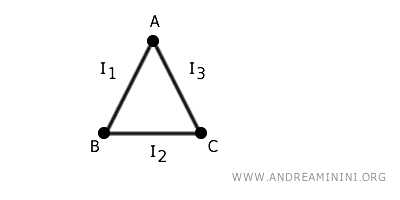
In questo modo ho creato una nuova struttura (grafo topologico) a partire da intervalli disgiunti, incollando i loro estremi a dei vertici.
In pratica, per creare il grafo ho "arrotolato" gli intervalli attorno ai vertici.
E così via.
