Topologia metrica

La topologia metrica su uno spazio $ X $ è la topologia generata dalla base formata dalle open ball definite da una distanza $ d $ su $ X $. E' anche detta topologia indotta dalla distanza $ d $.

In uno spazio metrico $ (X, d) $, dove $ d $ è una funzione che misura la distanza tra i punti di $ X $, posso definire una topologia metrica formata da insiemi aperti costruiti usando le "open ball".

Una "open ball" centrata in un punto $ x \in X $ con un raggio positivo $ \varepsilon $ è l'insieme di tutti i punti $ y $ di $ X $ che si trovano a meno di $ \varepsilon $ di distanza da $ x $:

$$ B_d(x, \varepsilon) = \{y \in X \mid d(x, y) < \varepsilon\}. $$

Nella topologia metrica, un insieme è aperto se può essere descritto come un'unione di queste palle aperte.

In altre parole, un insieme $ U \subset X $ è aperto nella topologia metrica indotta da $ d $ se e solo se, per ogni punto $ y \in U $, esiste un raggio $ \delta > 0 $ tale che la palla $ B_d(y, \delta) $ è contenuta in $ U $.

Un esempio pratico
Gli insiemi aperti nella topologia metrica
I vari tipi di metriche
Note a margine

Un esempio pratico

Considero lo spazio euclideo $\mathbb{R}$ in una dimensione, ossia una retta, con la distanza euclidea.

Lo spazio $\mathbb{R}$ è l'insieme di tutti i numeri reali.

La distanza $d$ tra due punti $x$ e $y$ in una retta è definita come:

$$ d(x, y) = |x - y| $$

Dove $|x - y|$ rappresenta il valore assoluto della differenza tra $x$ e $y$.

Questa distanza soddisfa tutte le proprietà di una metrica.

Ora, posso costruire delle "open ball" in $\mathbb{R}$ usando questa distanza.

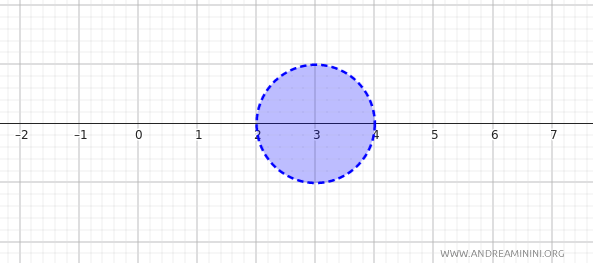
Ad esempio, considero il punto $x = 3$ e il raggio $\varepsilon = 1$.

La palla aperta centrata in $x = 3$ con raggio $1$ è:

$$ B_d(3, 1) = \{y \in \mathbb{R} \mid d(3, y) < 1\} = \{y \in \mathbb{R} \mid |3 - y| < 1\} $$

Risolvendo l’inequazione $ |3 - y| < 1 $, ottengo $2 < y < 4$. Quindi:

$$ B_d(3, 1) = (2, 4) $$

Questo significa che la palla aperta centrata in $3$ con raggio $1$ è l’intervallo aperto $(2, 4)$ sulla retta dei numeri reali.

esempio di open ball

Gli insiemi come $ (2, 4) $, $ (5, 7) $, o qualsiasi intervallo aperto $(a, b)$ in $\mathbb{R}$ possono essere visti come palle aperte o unioni di palle aperte rispetto alla distanza $d(x, y) = |x - y|$.

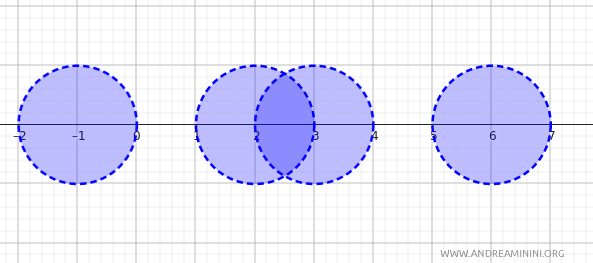
esempio di insiemi aperti in R

Questi intervalli formano una base per la topologia metrica di $\mathbb{R}$.

Nota. Nella topologia metrica di $\mathbb{R}$, un insieme è aperto se, per ogni punto in esso, è possibile trovare un intervallo aperto (una palla aperta) contenuto nell'insieme. Ad esempio, $(0, 5)$ è un insieme aperto, perché per ogni punto in $(0, 5)$ posso trovare un piccolo intervallo attorno a quel punto che è contenuto in $(0, 5)$.

In sintesi, usando la distanza $d(x, y) = |x - y|$ su $\mathbb{R}$, ottengo la topologia standard degli intervalli aperti, che chiamo topologia metrica su $\mathbb{R}$.

Gli insiemi aperti nella topologia metrica

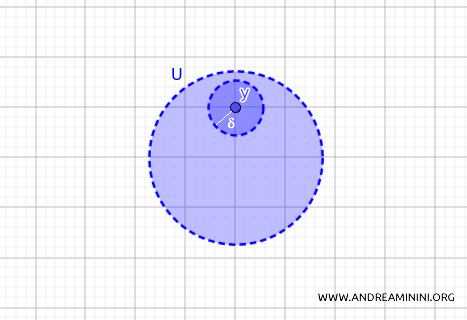
Nella topologia metrica un insieme $ U \subset X $ è un insieme aperto se per ogni punto $ y $ che appartiene a $ U $, esiste una open ball centrata in $ y $ (quindi una "zona intorno a $ y $" con un certo raggio $\delta$) che è completamente contenuta in $ U $.

In qualsiasi punto $ y $ in $ U $ di un insieme aperto $ U $ è sempre possibile trovare un piccolo "cerchio" (o sfera, se lo spazio è in più dimensioni) che resta completamente all'interno di $ U $.

Questo è ciò che rende l'insieme "aperto": ogni punto in $ U $ ha una zona intorno a sé che non "esce" da $ U $.

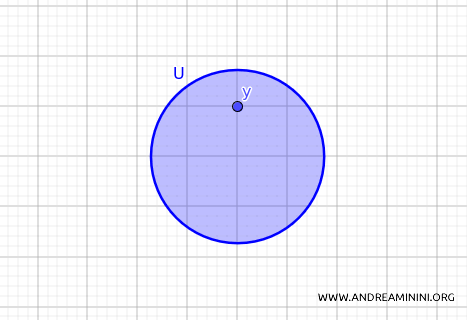
Ecco un esempio di insieme aperto in uno spazio metrico $ \mathbb{R}^2 $.

esempio di insieme aperto nella topologia metrica

Gli insiemi chiusi, invece, sono semplicemente le chiusure delle open ball, ossia gli insiemi che includono anche il bordo (o confine) oltre che ogni punto $ y $ al loro interno.

esempio di insieme chiuso

In breve, questo teorema formalizza l'idea di apertura in termini di "vicinanza" di ogni punto all'interno dell'insieme.

I vari tipi di metriche

Le topologie indotte possono essere basate su diverse metriche, non sono sulla metrica standard euclidea (circolare.

Ad esempio, esistono le metriche più applicate sul piano $ \mathbb{R}^2 $ sono:

Metrica standard (o metrica euclidea)
Questa metrica genera insiemi aperti di forma circolare, che sono le solite palle rotonde sul piano. Induce la topologia standard su $ \mathbb{R}^2 $. $$ d(p, q) = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2} $$
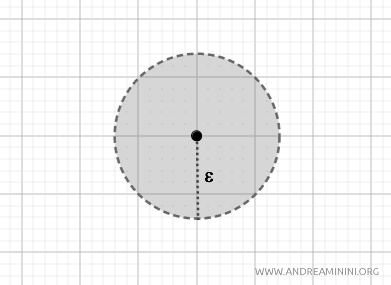
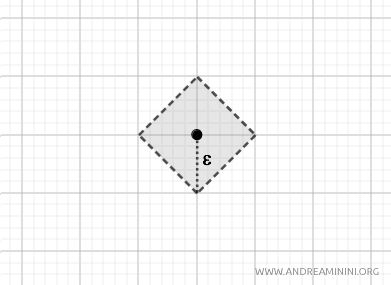
Metrica taxi (o metrica della distanza di Manhattan)
Con questa metrica, le palle aperte hanno la forma di un diamante (o rombo) e sono centrate in $ p $. Anche questa metrica induce la topologia standard su $ \mathbb{R}^2 $. $$ d_T(p, q) = |p_1 - q_1| + |p_2 - q_2|. $$
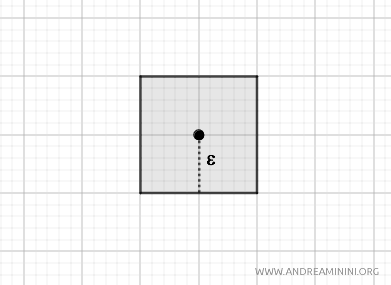
Metrica max
In questa metrica, le palle aperte hanno forma quadrata e sono centrate in $ p $, con lato di lunghezza pari a $ 2\varepsilon $. Anche questa metrica induce una topologia su $ \mathbb{R}^2 $.
$$ d_M(p, q) = \max\{|p_1 - q_1|, |p_2 - q_2|\} $$

Queste tre metriche, pur avendo diverse forme per le palle aperte (circolare, a diamante, e quadrata), inducono tutte una topologia metrica su $ \mathbb{R}^2 $.

Note a margine

Alcune note aggiuntive sulle topologie indotte da una metrica.

Teorema del confronto tra topologie metriche
Siano $d$ e $d'$ due metriche su un insieme $X$, che inducono rispettivamente le topologie $\mathcal{T}$ e $\mathcal{T}'$. La topologia $\mathcal{T}'$ è più fine di $\mathcal{T}$ se e solo se, per ogni $x \in X$ e ogni $\varepsilon > 0$, esiste un $\delta > 0$ tale che: $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$ dove $B_{d}(x, \varepsilon)$ e $B_{d'}(x, \delta)$ sono le palle aperte centrate in $x$ nelle due metriche.
In parole semplici, $\mathcal{T}'$ è più fine di $\mathcal{T}$ se ogni insieme aperto nella topologia di $d$ contiene almeno un insieme aperto della topologia di $d'$.

E così via.