La connessione in topologia
In topologia uno spazio è connesso se non è composto da insiemi aperti disgiunti. In altre parole, la connessione si riferisce alla proprietà di uno spazio in cui, dati due punti qualsiasi al suo interno, è sempre possibile viaggiare da un punto all'altro senza uscire dallo spazio.
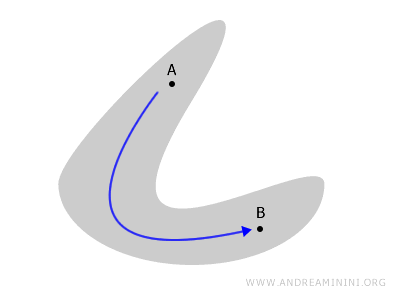
La connessione descrive come due parti di uno spazio topologico sono unite o separate.
Si tratta di una proprietà topologica perché è definita in termini di insiemi aperti.
E' uno dei concetti fondamentali della topologia insieme alla continuità.
La connessione è un concetto importante in molte aree della matematica, perché consente di comprendere come gli spazi sono strutturati e come le loro varie parti sono relazionate. Ad esempio, la connessione aiuta a classificare e analizzare le proprietà degli spazi topologici.
Un esempio pratico
Uno spazio (es. figura piana, poliedro, ecc.) è detto spazio connesso se presi due punti qualsiasi A e B al suo interno, esiste un percorso continuo che li collega senza uscire dallo spazio.

Viceversa, se esiste una separazione tra le sue parti, lo spazio non è connesso (spazio disconnesso).
Ad esempio, in questo caso lo spazio è composto da due parti disgiunte e qualsiasi percorso che collega i punti A e B esce dallo spazio.
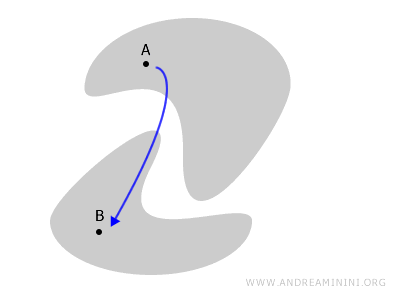
Secondo me, sugli spazi non connessi è opportuno soffermarsi un po' di più facendo un altro esempio pratico.
Quando uno spazio è disconnesso?
Il modo più semplice per capire cos'è uno spazio disconnesso è immaginare di avere due stanze non comunicanti separate da un muro che fanno parte dello stesso edificio (spazio).
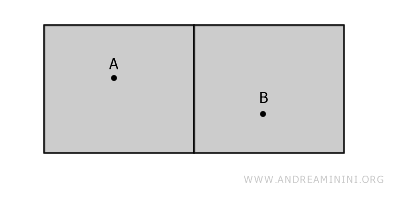
Queste due stanze possono essere viste come due insiemi aperti (non includono i confini ossia le pareti) e disgiunti (separati).
Le due stanze sembrano connesse ma non lo sono, perché qualsiasi percorso tra il punto A e il punto B esce dallo spazio perché passa per la parete e la parete non fa parte dello spazio.
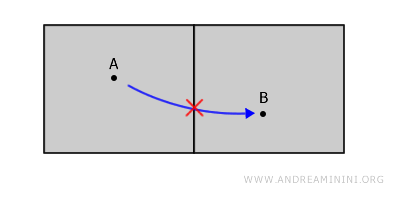
In conclusione, bisogna ricordarsi che in un insieme aperto i confini (le pareti) non fanno parte dello spazio.
La connessione locale
Si parla di connessione locale quando per ogni insieme aperto, anche se disgiunto da altre parti dello spazio, ogni punto ha un intorno connesso ovvero fa parte di un sottoinsieme aperto e connesso.
Ad esempio, considero uno spazio composto da insiemi aperti disgiunti.
E' il classico esempio delle due stanze non comunicanti separate da un muro all'interno di uno stesso edificio.

Lo spazio è disconesso perché i due punti A e B sono sono collegabili senza uscire dallo spazio, ovvero senza passare per le pareti.
Tuttavia, nel punto A c'è una connessione locale perché esiste un sottoinsieme che lo contiene in cui tutti i punti sono connessi.
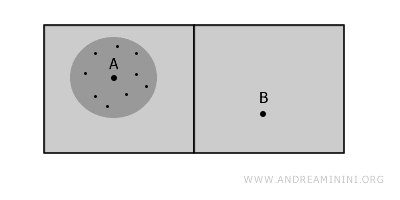
Allo stesso modo, anche nel punto B c'è una connessione locale.
Tipi di connessioni
Ci sono vari tipi di connessione, ma i due più comuni sono i seguenti:
- Connessione topologica
Uno spazio topologico $ X $ si dice connesso se non può essere suddiviso in due insiemi aperti disgiunti e non vuoti la cui unione sia l’intero spazio. In altre parole, non esiste una “separazione” dello spazio in due parti indipendenti.Esempio. Lo spazio (-1, 1) è connesso, mentre lo spazio (-1, 0) ∪ (0, 1) non è connesso, poiché esistono due insiemi aperti, disgiunti e non vuoti, (-1, 0) e (0, 1), la cui unione coincide con tutto lo spazio considerato.
Questa coppia di insiemi costituisce quindi una separazione dello spazio. - Connessione per archi (o per cammini)
Uno spazio topologico è detto connesso per archi se, per ogni coppia di punti A e B nello spazio, esiste un "arco", cioè un cammino continuo, che li collega senza lasciare lo spazio. Uno spazio connesso per archi è anche uno spazio connesso ma in generale non vale sempre il contrario.
Ad esempio, considero una figura piana chiusa. Per ogni coppia di punti interni A e B della figura posso tracciare con la penna un percorso continuo tra i due punti senza mai staccare la penna dal foglio o uscire dalla figura.
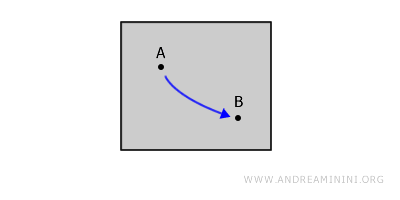
La differenza tra connessione per archi e per cammino. La connessione per archi (arc connectedness) è come la connessione per cammini, ma il cammino dev’essere iniettivo, cioè avviene senza “ripassare” due volte per lo stesso punto. - Connessione semplice
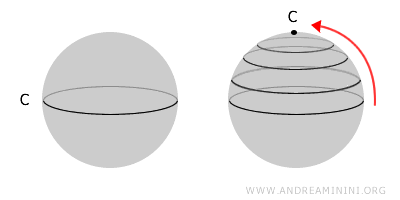
Uno spazio è semplicemente connesso quando ogni curva chiusa può essere trasformata in un punto. Questo significa che lo spazio topologico è composto da un unico "pezzo" e non ha buchi al suo interno. Uno spazio semplicemente connesso è sempre uno spazio connesso. Viceversa, uno spazio connesso non è detto che sia anche semplicemente connesso. In termini formali, in uno spazio topologico semplicemente connesso ogni cammino chiuso dello spazio è omotopo a un cammino costante che ha per immagine un punto.
Ad esempio, una sfera è semplicemente connessa perché ogni curva chiusa C posso deformarla fino ad ottenere un punto.
Viceversa una ciambella (spazio toroidale) non è semplicemente connessa perché la presenza del buco impedisce di trasformare il percorso chiuso C in un punto. In altre parole, la ciambella è uno spazio connesso, in quanto ogni coppia di punti A e B al suo interno è connessa, ma non è uno spazio semplicemente connesso.
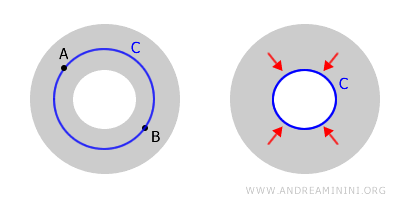
Uno spazio connesso ma non semplicemente connesso è detto spazio molteplicemente connesso. Ad esempio, la corona circolare è un esempio di spazio molteplicemente connesso. - Altri tipi di connessione più avanzati
In contesti più tecnici si incontra anche la connessione locale in cui ogni punto ha un intorno connesso.
Osservazioni
Alcune osservazioni personali e note a margine
- Nell'insieme dei numeri reali gli unici spazi connessi sono gli intervalli.
E così via.
