Insiemi né aperti, né chiusi
In topologia un insieme può essere nè aperto e nè chiuso, quando non soddisfa sia le caratteristiche degli insiemi aperti che quelle degli insiemi chiusi.
Questa tipo di insieme può verificarsi in una topologia quando l'insieme non è definito come insieme aperto e non è il complemento di un insieme aperto.
Quindi, l'insieme non è neanche un insiemi chiuso.
Nota. E' un tipo di insieme difficile da immaginare se si pensa alla topologia comune dei numeri reali. Tuttavia, è del tutto possibile in altre topologie più complesse. Per spiegare meglio questo concetto credo sia opportuno fare un esempio pratico.
Un esempio pratico
Prendo in considerazione l'insieme X={a,b,c,d} e la topologia T che individua i seguenti insiemi aperti: {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, Ø.
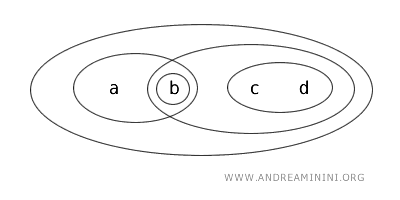
Ora considero il sottoinsieme {b,c} degli elementi dell'insieme.
- L'insieme {b,c} non è un "insieme aperto" perché la topologia T non lo definisce esplicitamente come insieme "aperto".
- L'insieme {b,c} non è il complemento di nessun insieme aperto nella topologia T. Quindi, non è nemmeno un "insieme chiuso".
In conclusione, secondo la topologia T l'insieme {b,c} è un insieme né aperto, né chiuso.
E così via.
Risposte rapide
- Nella topologia dei numeri reali, è comune incontrare insiemi come [0, 1), che non sono né aperti né chiusi. È corretto?
L'intervallo \([0, 1)\) nella topologia dei numeri reali (con la topologia standard) presenta le seguenti caratteristiche:- Non aperto: Un intervallo è considerato aperto se ogni punto al suo interno possiede un intorno completamente contenuto nell'intervallo stesso. Nel caso di \([0, 1)\), il punto \(0\) non soddisfa questa condizione, poiché ogni suo intorno include punti inferiori a \(0\), che non appartengono all'intervallo.
- Non chiuso: Un intervallo è chiuso se contiene tutti i suoi punti limite. Per \([0, 1)\), il punto \(1\) è un punto limite ma non è incluso nell'intervallo, rendendolo quindi non chiuso.
