Insiemi clopen
Un insieme è detto "clopen" se è sia aperto che chiuso rispetto alla topologia specificata.
In altre parole, un insieme è "clopen" se soddisfa contemporaneamente le definizioni di aperto e chiuso nella topologia considerata.
Il termine "clopen" deriva dalla combinazione delle parole "closed" (chiuso) e "open" (aperto).
Questi insiemi hanno la caratteristica di possedere le caratteristiche sia degli insiemi aperti che degli insiemi chiusi.
Questo può accadere se in una topologia sia l'insieme considerato che il suo complemento sono insiemi aperti.
Nota. Sono particolarmente insoliti se visti nell'insieme dei numeri reali ma possono esistere in topologia. Sono interessanti perché possono avere proprietà utili in topologia e possono giocare un ruolo significativo nello studio della struttura topologica di uno spazio.
Un esempio pratico
Considero l'insieme X={a,b,c,d} nella topologia T.
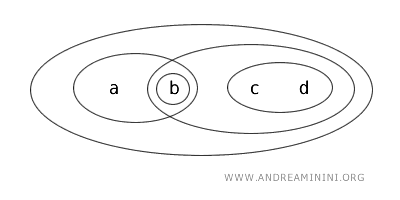
Secondo la topologia T sono "insiemi aperti" i seguenti insiemi: {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, Ø.
Quindi, il sottoinsieme {a,b} è un "insieme aperto" per definizione della stessa topologia T.
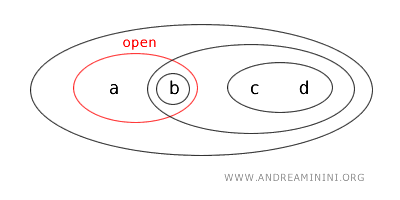
Tuttavia, a ben guardare l'insieme {a,b} è anche il complemento dell'insieme aperto {c,d}
$$ X - \{ c,d \} = \{a , b \} $$
Il complemento di un insieme aperto è sempre un insieme chiuso.
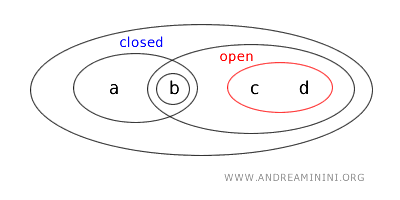
Quindi, l'insieme {a,b} è contemporaneamente anche un "insieme chiuso".
In conclusione, nella topologia T l'insieme {a,b} è sia aperto che chiuso ovvero è un insieme "clopen".
L'insieme vuoto e l'intero insieme sono clopen
In ogni topologia sull'insieme X, l'intero insieme (X) e l'insieme vuoto (∅) sono sempre insiemi clopen, ovvero sia aperti che chiusi.
Per chiarire, un set è definito come "clopen" se è sia aperto che chiuso nella topologia considerata.
Ora, basta rileggere le definizioni di insieme aperto e di insieme chiuso.
Nella definizione topologica dell'insieme aperto, l'insieme vuoto (∅) e l'intero insieme (X) sono considerati sempre come insiemi "aperti".
Inoltre, secondo la definizione di insieme chiuso, un insieme è considerato "chiuso" se il suo complemento è aperto.
Mettendo insieme questi concetti deduco che:
- Insieme vuoto (∅)
L'insieme vuoto è considerato aperto per la definizione stessa di topologia. D'altra parte è anche chiuso perché il suo complemento X $ \setminus ∅=X $ (l'intero insieme) è un insieme aperto. Quindi è sia aperto che chiuso (clopen). - Intero insieme (X)
L'intero insieme è considerato aperto per la definizione stessa di topologia. Inoltre, è anche chiuso perché il suo complemento $ X \setminus X=∅ $ (l'insieme vuoto) è un insieme aperto. Quindi è sia aperto che chiuso (clopen).
Quindi, in ogni topologia, sia l'intero insieme X che l'insieme vuoto ∅ sono sempre clopen sets.
E così via.
