Equazione della bisettrice del piano cartesiano
La bisettrice del piano cartesiano è una retta passante per l'origine con i punti equidistanti dagli assi cartesiani. $$ |y| = |x| $$
L'ascissa e l'ordinata della bisettrice sono uguali in valore assoluto.
Il piano cartesiano ha due bisettrici
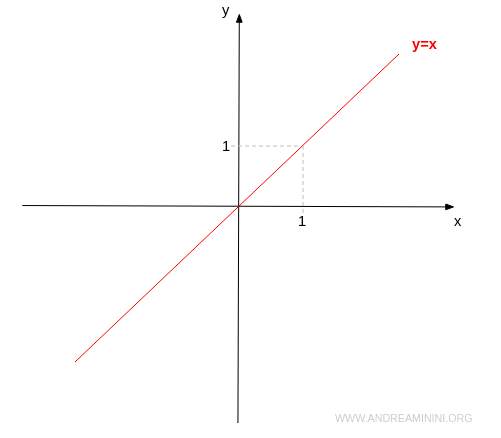
- La bisettrice del primo e del terzo quadrante
Le coordinate (x,y) dell'equazione della bisettrice del I e III quadrante sono caratterizzate da ascissa e ordinata dello stesso segno e valore $$ y=x $$ Quindi, l'equazione ha infinite soluzioni. Ogni punto della bisettrice è una soluzione.
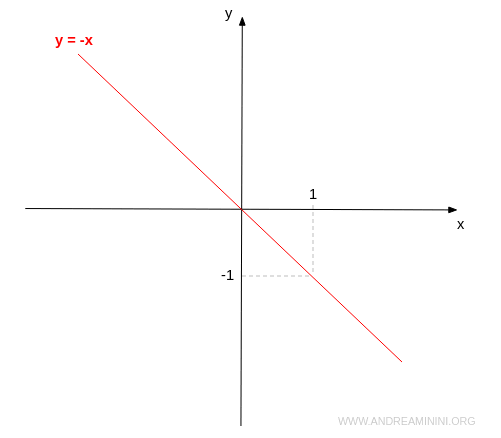
- La bisettrice del secondo e del quarto quadrante
Le coordinate (x,y) dell'equazione della bisettrice del II e IV quadrante sono caratterizzate da valori opposti. $$ y=x $$ Anche questa equazione ha infinite soluzioni. Ogni punto della bisettrice è una soluzione dell'equazione.
Le due bisettrici del piano cartesiano sono due casi particolari dell'equazione della retta.
