Teorema della retta perpendicolare a un piano

Dati un piano \( \alpha \) e un punto \( P \), esiste un'unica retta \( r \) passante per il punto \( P \) e perpendicolare al piano \( \alpha \).

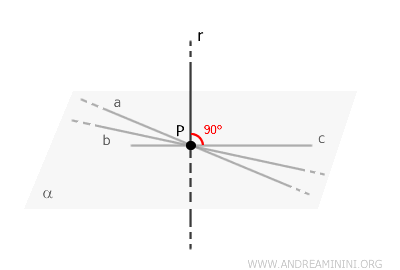
Ogni piano nello spazio ha un'unica direzione perpendicolare, che è definita dal vettore normale del piano.

La retta \( r \) è quella che passa per il punto \( P \) e segue la direzione del vettore normale al piano \( \alpha \).

Nota. La condizione di unicità deriva dal fatto che il vettore normale è unico (a meno di moltiplicazione per uno scalare), quindi esiste una sola retta con questa proprietà.

La dimostrazione

Considero il piano \( \alpha \) e scelgo un punto qualsiasi \( P \) appartenente al piano.

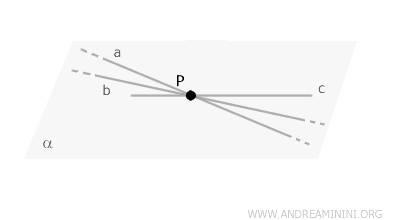
Un piano contiene infiniti punti e infinite rette complanari $ a $, $ b $, $ c $...

Per definizione, una retta è perpendicolare al piano \( \alpha \) se forma un angolo retto con tutte le rette passanti per \( P \) appartenenti al piano \( \alpha \).

Quindi, dato il punto \( P \), posso sempre immaginare una retta perpendicolare $ r $ che parte da \( P \) e forma un angolo retto con tutte le rette contenute nel piano \( \alpha \).

A questo punto devo dimostrare l'unicità della retta perpendicolare $ r $, ossia che esiste una sola retta con questa proprietà.

Per ipotesi assurda suppongo che esistano due rette \( r \) e \( r' \) passanti per \( P \) e perpendicolari al piano \( \alpha \).

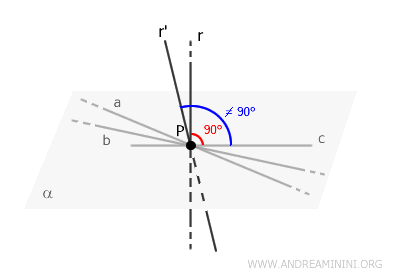
Tuttavia, se così fosse, almeno una delle due rette \( r \) e \( r' \) dovrebbe formare un angolo diverso da \( 90^\circ \) con le rette del piano, altrimenti sarebbero coincidenti, violando una delle condizioni necessarie della perpendicolarità al piano

Questo implica che \( r \) e \( r' \) non possono essere distinte e si sovrappongono. Sono rette coincidenti.

Quindi, esiste una sola retta che passa per il punto \( P \) ed è perpendicolare al piano \( \alpha \).

E così via.