Punto

Nella geometria euclidea, un punto è uno degli enti fondamentali, insieme alla retta e al piano.

E' un concetto primitivo perché non viene definito in termini di altri concetti geometrici. Quindi, non ha una ha una definizione formale in termini di altri concetti geometrici

In termini intuitivi, un punto è visto come un oggetto che non ha dimensioni (lunghezza, larghezza, altezza), né una forma e non è ulteriormente divisibile in parti più piccole. Negli "Elementi" Euclide definì il punto come "ciò che non ha parti".

Sebbene non abbia dimensioni, graficamente un punto viene rappresentato come un piccolo segno, come un piccolo cerchio o un punto, per indicare la sua posizione.

È però importante non confondere il simbolo utilizzato per rappresentarlo (ad esempio, un cerchio) con il punto stesso. Il simbolo ha una dimensione fisica, mentre il punto è adimensionale ed è un concetto geometrico astratto che non può essere rappresentato fisicamente in modo perfetto. Quindi, quando disegno un punto su un foglio di carta, in realtà sto semplicemente rappresentando una piccola macchia che approssima l'idea di punto.

In geometria il punto viene  rappresentato con una lettera maiuscola, ad esempio \( A \), \( B \), \( C \).

Un punto può essere considerato come un'indicazione di una posizione nello spazio.

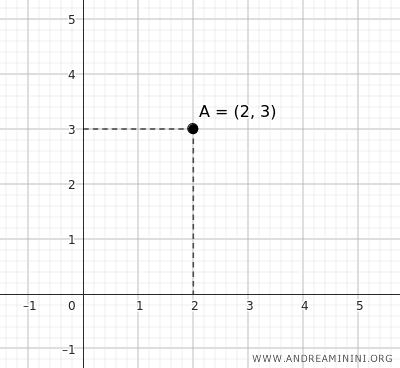
Nel piano cartesiano bidimensionale, il punto è descritto da una coppia di coordinate \((x, y)\).

Ad esempio, il punto A si trova alle coordinate (2,3) del piano cartesiano, rappresenta una posizione precisa sul piano a 2 unità lungo l'asse x e 3 unità lungo l'asse y.

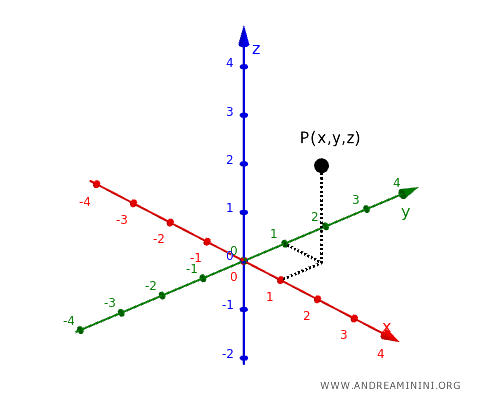
Nello spazio tridimensionale, invece, un punto è descritto da una terna di coordinate \((x, y, z)\).

Nei postulati di Euclide, i punti sono utilizzati per definire altri concetti fondamentali:

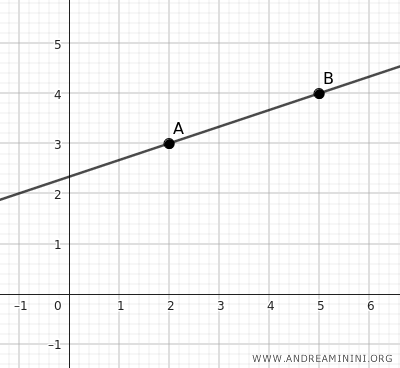
Ad esempio, una retta è determinata da due punti distinti.

Qualsiasi retta può essere pensata come una collezione infinita di punti allineati nella stessa direzione.

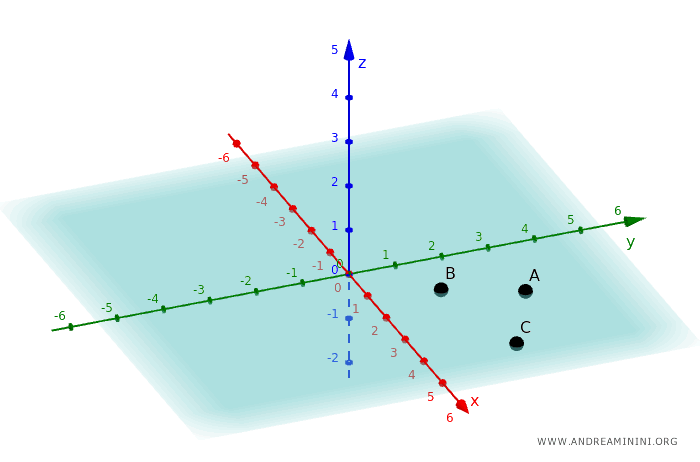
Un piano è, invece, determinato da tre punti non allineati. E' una superficie bidimensionale composta da infiniti punti che si estende all'infinito.

In generale, i punti sono utilizzati per costruire anche figure geometriche più complesse, come segmenti, angoli, poligoni e curve.

E così via.