Problema di geometria 2

In questo triangolo rettangolo è noto solo l'angolo del vertice C che è pari a 52° e le bisettrici degli angoli ai vertici A e B. Devo calcolare la somma delle ampiezze degli angoli x e y.

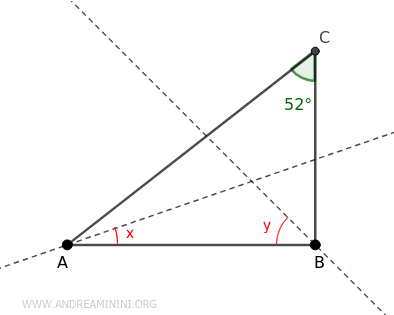
Poiché si tratta di un triangolo rettangolo, si comprende subito che l'angolo al vertice B è un angolo retto (90°) anche se non è indicato esplicitamente nella figura.

$$ A \hat{B} C = 90° $$

Sapendo che la bisettrice divide l'angolo $ A \hat{B} C $ a metà, deduco che l'ampiezza dell'angolo y posso ottenerlo dividendo l'angolo al vertice B per due.

$$ y = \frac{A \hat{B} C }{2} $$

$$ y = \frac{90°}{2} $$

$$ y = 45° $$

La somma degli angoli interni di un triangolo è sempre uguale a un angolo piatto (180°).

$$ B \hat{A} C + A \hat{B} C + A \hat{C} B = 180° $$

Due angoli del triangolo già li conosco, quindi posso calcolare il terzo angolo per differenza.

$$ B \hat{A} C + 90° + 52° = 180° $$

$$ B \hat{A} C = 180° - 90° - 52°$$

$$ A \hat{B} C = 38° $$

Una volta noto l'angolo $ A \hat{B} C $ ottengo anche l'angolo x, perché la bisettrice taglia a metà l'angolo.

$$ x = \frac{A \hat{B} C} {2} $$

$$ x = \frac{38°}{2} $$

$$ x = 19° $$

Quindi, gli angoli x e y valgono rispettivamente x=19 e y=45.

La loro somma è pari a x+y

$$ x+y = 19° + 45° $$

$$ x+y = 64° $$

In conclusione, la somma delle ampiezze degli angoli x+y è 64°

Questa è la soluzione del problema.

E così via.