Funzioni dispari

Cosa sono le funzioni dispari

Una funzione è detta funzione dispari se per qualunque x del suo dominio vale $$ f(-x)=-f(x) \ \ \ \forall \ x \ \in D $$

Il grafico di una funzione dispari è simmetrico rispetto all'origine degli assi, perché per ogni punto P(x,y) esiste un punto opposto P(-x,-y).

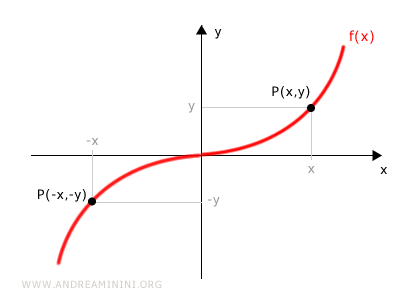
Come riconoscere se una funzione è dispari?

Ci sono due modi per capirlo

• Dal punto di vista analitico devo il valore della funzione f(-x) rispetto al valore opposto -x e confrontarlo con il valore -f(x). Se i valori coincidono, la funzione è dispari. $$ f(-x) = -f(x) $$

  Esempio. Considero la funzione f(x)=x³. Sostituisco la x con il suo opposto -x e verifico se ottengo la funzione -f(x). $$ f(-x)=(-x)^3 = -x^3 = -f(x) $$ L'espressione f(-x) coincide con -f(x). Quindi, la funzione è dispari.

• Dal punto di vista grafico rifletto il grafico della funzione in verticale rispetto al semiasse negativo delle x, se i due grafici g(x) e f(x) sono simmetrici rispetto all'asse y allora la funzione è dispari.
  

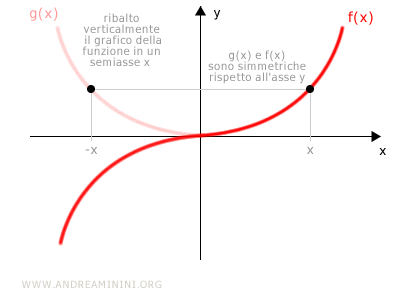
Nota. Se una funzione non è dispari, non è detto che sia pari. E viceversa. Ad esempio, la funzione f(x)=x+x² non è né dispari $$ f(-x)=(-x)+(-x)^2 = -x+x^2 \ne -f(x) = -x -x^2 $$ né pari. $$ f(-x)=(-x)+(-x)^2 = -x+x^2 \ne f(x) = x+x^2 $$

Un esempio pratico

Un esempio di funzione dispari è la funzione seno

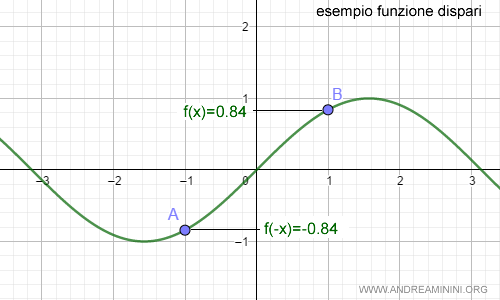
Per qualunque valore x del dominio della funzione seno vale la relazione f(-x)=-f(x)

Nota. Ad esempio, in x=1 la funzione seno è sin(1)=0.84. Se calcolo la funzione rispetto a -1 ottengo sin(1)=0.84. E' lo stesso valore che ottengo quando calcolo -sin(x)=-0.84. Quindi, f(-x)=-f(x).

Esempio 2

Un altro esempio di funzione dispari è la funzione x³.

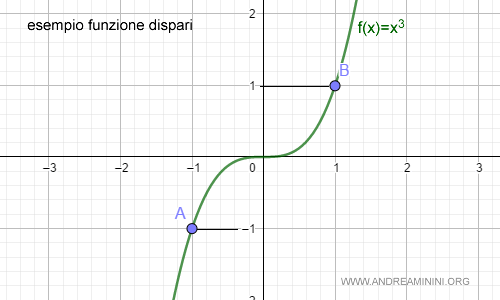
Per qualunque valore x del dominio della funzione vale la relazione f(-x)=-f(x).

Nota. In generale, se una funzione ha soltanto potenze di x con esponente dispari, allora la funzione è dispari

Esempio 3

Devo verificare analiticamente se questa funzione è dispari

$$ f(x) = x^2+x $$

Sostituisco la x con il suo opposto -x nell'espressione della funzione

$$ f(-x) = (-x)^2+(-x) = x^2 - x $$

Il risultato è diverso dall'opposto della funzione -f(x)

$$ -f(x) = -(x^2+x) = -x^2-x $$

Quindi la funzione non è una funzione dispari.

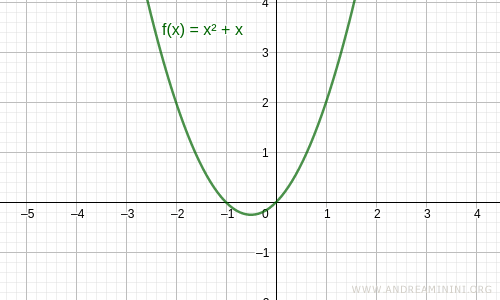
Nota. La funzione f(x)=x²+x non è nemmeno una funzione pari perché non è simmetrica rispetto all'asse y.

E così via.