Sistema di equazioni impossibile

Un sistema di equazioni è impossibile se non ammette soluzioni.

In particolar modo un sistema lineare (1° grado)

$$ \begin{cases} a_1x + b_1y = c_1 \\ \\ a_2x + b_2y = c_2 \end{cases} $$

non ha soluzioni se si verificano queste due condizioni

• il rapporto tra i coefficienti delle variabili x e y delle due equazioni è uguale $$ \frac{a_1}{a_2} = \frac{b_1}{b_2} $$
• il rapporto tra i coefficienti delle variabili x e y non è uguale al rapporto dei termini noti $$ \frac{a_1}{a_2} = \frac{b_1}{b_2} \ne \frac{c_1}{c_2} $$

Questa semplice verifica mi permette di capire se un sistema lineare non ha soluzioni senza dover svolgere alcun calcolo.

Nota. Se i rapporti a₁/a₂ ≠ b₁/b₂ sono diversi, le rette hanno un coefficiente angolare diverso a₁/b₁ ≠ a₂/b2, ossia una diversa inclinazione. Due rette con diversa inclinazione sono rette incidenti perché si incontrano in un punto. Quindi il sistema ha una soluzione (sistema determinato). Se i rapporti a₁/a₂ = b₁/b₂ sono uguali al rapporto dei termini noti c₁/c₂ allora le due rette sono rette coincidenti. In questo caso le equazioni hanno infiniti punti in comune e il sistema ha infinite soluzioni (sistema indeterminato).

Un esempio pratico

Devo capire se questo sistema lineare è determinato

$$ \begin{cases} 2x + 4y = 3 \\ \\ 4x + 8y = -5 \end{cases} $$

Verifico se il rapporto tra i coefficienti delle variabili x e y è uguale

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} $$

Sapendo che i coefficienti delle variabili x e y sono a₁=2, b₁=4, a₂=4, b₂=-8

$$ \frac{2}{4} = \frac{4}{8} $$

$$ \frac{1}{2} = \frac{1}{2} $$

Il rapporto tra i coefficienti delle variabili x e y è uguale.

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{1}{2} $$

La prima condizione è soddisfatta.

Nota. se il rapporto tra i coefficienti fosse diverso l'esercizio finirebbe qui. Se la prima condizione non è soddisfatta, è del tutto inutile verificare la seconda condizione.

Ora per capire se il sistema non ha soluzioni devo verificare se il rapporto dei coefficienti è diverso dal rapporto dei termini noti.

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} \ne \frac{c_1}{c_2} $$

Conosco già il rapporto tra i coefficienti a₁/a₂=b₁/b₂=1/2

$$ \frac{1}{2} \ne \frac{c_1}{c_2} $$

Sapendo che i termini noti delle equazioni sono c₁=3 e c₂=-5

$$ \frac{1}{2} \ne - \frac{3}{5} $$

La seconda condizione è soddisfatta.

Pertanto, posso affermare con certezza che il sistema non ha soluzioni ossia è un sistema impossibile.

Verifica. Utilizzo il metodo grafico per verificare se il sistema di equazioni lineari non ammette soluzioni. Le rette delle due equazioni sono parallele. Quindi, le rette non hanno punti in comune. Questo vuol dire che il sistema non ha soluzioni.

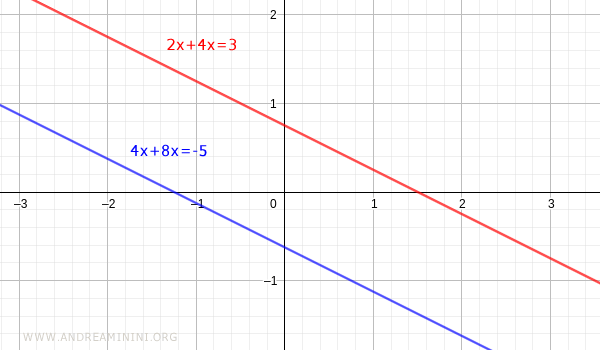
La dimostrazione

Considero un sistema di equazioni di 1° grado (lineare) con due variabili indipendenti x e y

$$ \begin{cases} a_1x + b_1y = c_1 \\ \\ a_2x + b_2y = c_2 \end{cases} $$

Un sistema lineare con due variabili posso rappresentarlo sul piano cartesiano xy.

Ogni equazione lineare del sistema individua una retta sul piano.

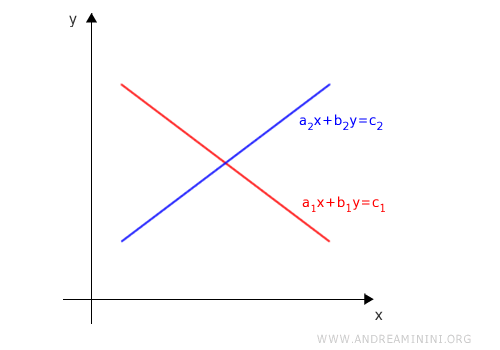
Nota. I punti della retta di un'equazione sono i valori (x;y) che soddisfano l'equazione.

Se le due rette si intersecano le due equazioni hanno un punto in comune.

Quindi il sistema ha una soluzione (sistema determinato).

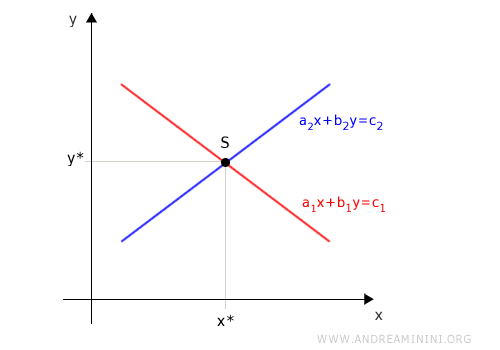
Pertanto, un sistema di equazioni non ammette soluzioni solo se le equazioni non si intersecano.

Questo accade solo nel caso in cui le due rette sono rette parallele.

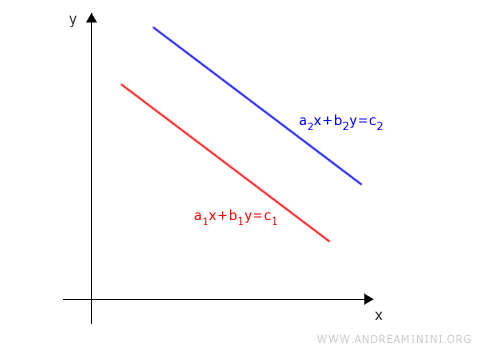
Due rette sono parallele se hanno lo stesso coefficiente angolare e un termine noto diverso.

Scrivo le equazioni del sistema in forma esplicita

$$ \begin{cases} y = -\frac{a_1}{b_1} x + \frac{c_1}{b_1} \\ \\ y = -\frac{a_2}{b_2} x + \frac{c_2}{b_2} \end{cases} $$

Se le rette sono parallele i coefficienti angolari delle due rette -a₁/b₁ e -a₂/b₂ devono essere uguali

$$ -\frac{a_1}{b_1} = -\frac{a_2}{b_2} $$

Per la proprietà invariantiva moltiplico entrambi i membri per -1

$$ (-1) \cdot -\frac{a_1}{b_1} = -\frac{a_2}{b_2} \cdot (-1) $$

$$ \frac{a_1}{b_1} = \frac{a_2}{b_2} $$

Poi moltiplico entrambi i membri dell'equazione per b₁/a₂ e semplifico

$$ \frac{a_1}{b_1} \cdot ( \frac{b_1}{a_2} ) = \frac{a_2}{b_2} \cdot ( \frac{b_1}{a_2} ) $$

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} $$

Nota. In alcuni testi la stessa condizione è scritta in forme algebriche equivalenti. Ad esempio $$ a_1 b_2 = a_2 b_1 $$ oppure $$ a_1 b_2 - a_2 b_1 = 0 $$ Dal punto di vista geometrico il significato è sempre lo stesso.

Tuttavia, l'uguaglianza dei coefficienti angolari non basta a garantire che le rette siano parallele.

Ad esempio, due rette con lo stesso coefficiente angolare potrebbero anche essere coincidenti.

Due rette coincidenti hanno infiniti punti in comune. In questo caso il sistema ha infinite soluzioni (sistema indeterminato).

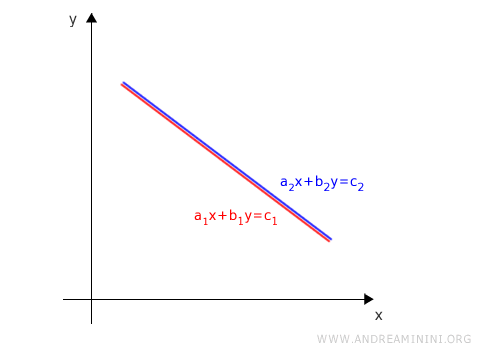
Per evitare che le rette siano coincidenti il rapporto dei coefficienti a₁/a₂=b₁/b₂ deve essere diverso dal rapporto dei termini noti c₁/c₂.

$$ \frac{a_1}{a_2} = \frac{b_1}{b_2} \ne \frac{c_1}{c_2} $$

In questo modo le rette sono parallele, non hanno punti in comune e il sistema è senza soluzioni (sistema impossibile).

E' quello che volevo dimostrare.

E così via.