La funzione derivabile in un punto
Una funzione è derivabile in un punto c quando i due limiti sinistro e destro del rapporto incrementale esistono e hanno lo stesso valore. $$ f'(x) = \lim_{Δx \rightarrow 0^-} \frac{f(x+Δx)-f(x)}{Δx} \\ \\ f'(x) = \lim_{Δx \rightarrow 0^+} \frac{f(x+Δx)-f(x)}{Δx} $$
Il limite sinistro del rapporto incrementale è detto derivata sinistra.
$$ f'(x) = \lim_{Δx \rightarrow 0^-} \frac{f(x+Δx)-f(x)}{Δx} $$
Il limite destro del rapporto incrementale è detto derivata destra.
$$ f'(x) = \lim_{Δx \rightarrow 0^+} \frac{f(x+Δx)-f(x)}{Δx} $$
Possono verificarsi due situazioni
- Se i due limiti esistono e coincidono, la funzione è derivabile nel punto c.
- Se i due limiti non coincidono, la funzione non è derivabile nel punto c.
I punti dove la funzione f(x) non è derivabile sono detti punti singolari.
Un esempio pratico
Ho la funzione f(x) del valore assoluto |x|
$$ f(x) = |x| $$
Per verificare se è derivabile in x=0 calcolo il limite destro.
$$ f'(0) = \lim_{Δx \rightarrow 0^+} \frac{f(x+Δx)-f(x)}{Δx} $$
$$ f'(0) = \lim_{Δx \rightarrow 0^+} \frac{|x+Δx|-|x|}{Δx} $$
$$ f'(0) = \lim_{Δx \rightarrow 0^+} \frac{|0+Δx-0|}{Δx} $$
$$ f'(0) = \lim_{Δx \rightarrow 0^+} \frac{|Δx|}{Δx} = +1 $$
Poiché Δx si avvicina sempre più a zero da destra, senza mai raggiungerlo, il limite è sicuramente un valore positivo ed è uguale a +1.
Ora calcolo il limite sinistro in x=0
$$ f'(0) = \lim_{Δx \rightarrow 0^-} \frac{f(x+Δx)-f(x)}{Δx} $$
$$ f'(0) = \lim_{Δx \rightarrow 0^-} \frac{|x+Δx|-|x|}{Δx} $$
$$ f'(0) = \lim_{Δx \rightarrow 0^-} \frac{|0+Δx-0|}{Δx} $$
$$ f'(0) = \lim_{Δx \rightarrow 0^-} \frac{|Δx|}{Δx} = -1 $$
In questo caso Δx tende a x=0 da sinistra. Pertanto è sempre un valore negativo e il limite del rapporto incrementale è -1.
Conclusione
Il limite destro e sinistro del rapporto incrementale non coincidono in x=0.
$$ f'(0^+) = \lim_{Δx \rightarrow 0^+} \frac{|Δx|}{Δx} = +1 $$
$$ f'(0^-) = \lim_{Δx \rightarrow 0^-} \frac{|Δx|}{Δx} = -1 $$
Pertanto, anche se le rette si toccano, nel punto x=0, la funzione f(x)=|x| non è derivabile perché i due limiti destro e sinistro non coincidono (+1 ≠ -1).
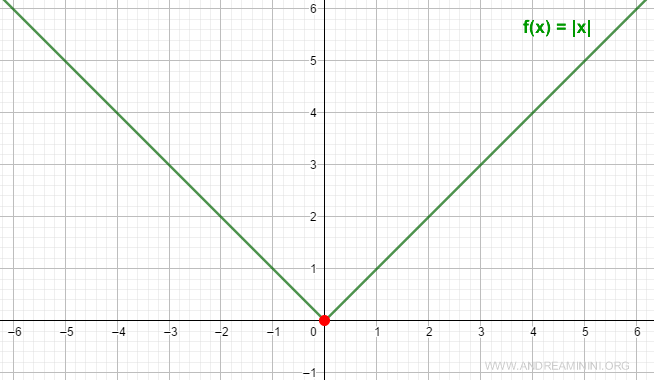
Nota. Questo esempio dimostra anche che la continuità della funzione in un punto è una condizione necessaria ma non sufficiente alla derivabilità. La funzione |x| è continua in x=0 ma non è derivabile in x=0.
E così via.
