La derivata di una funzione

La definizione di derivata

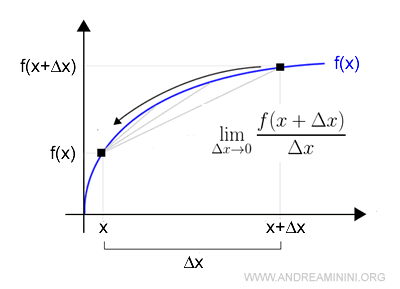
La derivata di una funzione f(x) in un punto x è il limite del rapporto incrementale

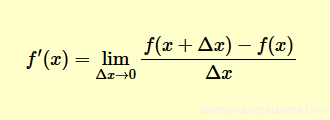
Il valore del limite del rapporto incrementale è detta derivata prima e si indica con f'(x).

Il limite del rapporto incrementale è invece detto operazione di derivazione.

Esempio

La derivata prima può essere indicata anche in altri modi o con altre notazioni

$$ f'(x)=Df=\frac{dy}{dx}=y' $$

Il simbolo dy/dx è detta notazione di Leibniz.

Nota. La derivata prima f'(x) è a tutti gli effetti un'altra funzione e a sua volta può essere derivata. La derivata della derivata è detta derivata seconda e si indica con f"(x) e così via.

Le condizioni della derivabilità

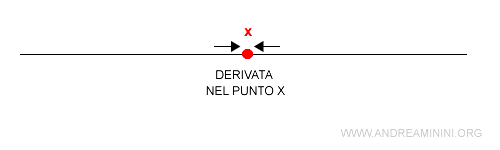
Una funzione f(x) definita nell'intervallo (a,b) è una funzione derivabile in un punto x se esiste il limite del rapporto incrementale in x per h tendente a zero.

Una funzione è derivabile in un intervallo aperto (a,b) se è derivabile in ogni punto x compreso tra gli estremi a e b esclusi ossia x ∈ (a,b) .

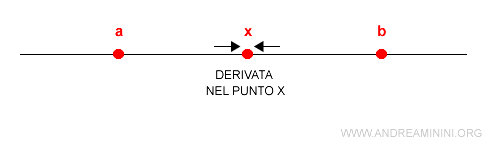
Una funzione è derivabile in un intervallo chiuso [a,b] se è derivabile in ogni punto x ∈ [a,b] e se esiste la derivata destra nel punto a e la derivata sinistra nel punto b.

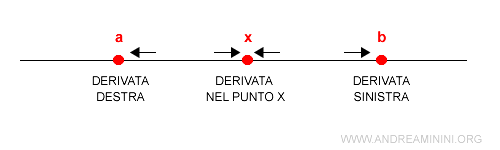
I punti dove la funzione non è derivabile sono detti punti singolari.

La derivata sinistra e la derivata destra

Può comunque accadere che la funzione non sia derivabile nel punto x, ma lo sia negli altri punti a sinistra o a destra di x.

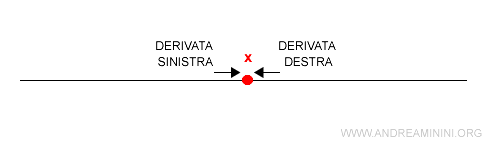
In questi casi i valori finiti dei limiti sono detti derivata sinistra e derivata destra di x.

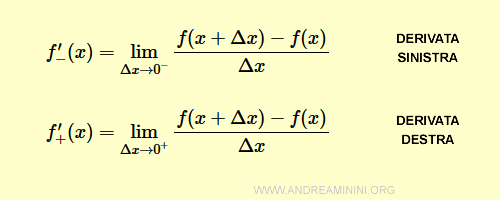
Qual è la differenza?

Nella derivata sinistra l'incremento Δx tende a 0 da sinistra ed è un numero negativo Δx<0.

Nella derivata destra, invece, l'incremento Δx tende a 0 da destra ed è un numero positivo Δx>0.

Se una funzione è derivabile nel punto x allora la derivata destra e sinistra esistono e hanno lo stesso valore. $$ f'(x) = f'_-(x)=f'_+(x) $$

Un esempio pratico

Questa funzione non è definita per x=0

$$ \frac{1}{x} $$

Nel punto x=0 la funzione f(x) non è derivabile.

Quindi x=0 è un punto singolare della funzione f(x).

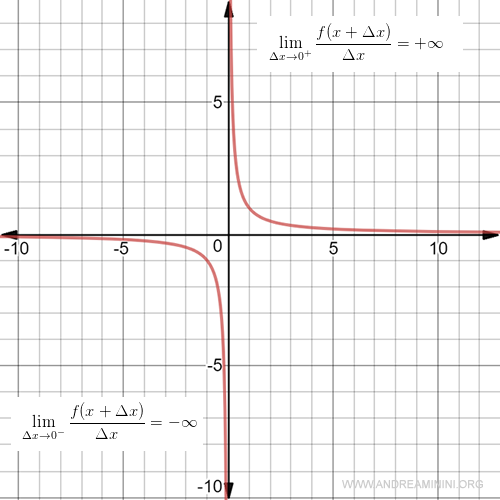
Tuttavia, in x=0 la funzione f(x) ha sia la derivata sinistra che la derivata destra.

Il limite della derivata sinistra tende a meno infinito

$$ f'_-(x) = \lim_{Δx \rightarrow 0^-} \frac{f(x+Δx)-f(x)}{Δx} = - \infty $$

Il limite della derivata destra tende a più infinito

$$ f'_+(x) = \lim_{Δx \rightarrow 0^+} \frac{f(x+Δx)-f(x)}{Δx} = + \infty $$

In questo modo posso studiare il comportamento della funzione anche nei punti in cui non è definita.

Corollari sulle derivate

• Se la funzione è derivabile in x e la derivata f'(x) è un numero finito, allora la derivata sinistra e la derivata destra esistono e sono uguali alla derivata prima

  $$ se \:\: f'(x) = l \:\:\:\: \Rightarrow \:\:\:\:f'(x) = f'_-(x) = f_+(x) $$

  Viceversa, se la funzione non è derivabile in x, la derivata sinistra e la derivata destra potrebbero anche essere diverse o esisterne soltanto una.

La notazione di Leibniz

Una delle notazioni matematiche più usate nel calcolo delle derivate è la notazione di Leibniz.

$$ \frac{dy}{dx} $$ oppure $$ \frac{δy}{δx} $$

Al numeratore è indicata la funzione ( codominio).

Al denominatore è indicata la variabile di derivazione ( dominio ), ossia quella per cui voglio derivare la funzione.

Nota. La notazione di Leibniz è utile quando la funzione è composta da diverse variabili ed è necessario specificare qual è la variabile di derivazione. Se la variabile di derivazione è soltanto una, consiglio di usare una notazione più sintetica come y''.

E così via