La derivata di una costante
La derivata di una funzione costante è nulla. $$ f(x)=k \:\: \rightarrow \:\: f'(x)=0 $$
La spiegazione è facilmente dimostrabile
Dimostrazione
Data una funzione f(x) definita nell'intervallo (a,b) e un generico punto x del dominio.
$$ f(x)= k $$
Per qualsiasi valore del dominio, la funzione f(x) restituisce sempre lo stesso valore k.
Il grafico della funzione è il seguente:
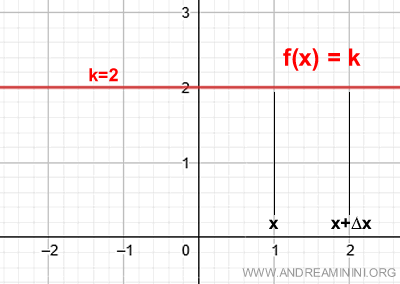
Per ottenere la derivata della funzione, devo calcolare il limite del rapporto incrementale
$$ \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} $$
So già che
- f(x)=k
- f(x+Δx)=k
Quindi, posso riscrivere il rapporto incrementale in questa forma:
$$ \lim_{\Delta x \rightarrow 0} \frac{k-k}{\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{0}{\Delta x} = 0 $$
Ho così dimostrato che la derivata di una costante è zero.
Un esempio pratico
Data la seguente funzione:
$$ f(x) = 2 $$
Calcolo il limite del rapporto incrementale per Δx tendente a zero.
$$ \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} $$
Sapendo che
- f(x)=2
- f(x+Δx)=2
Il limite del rapporto incrementale diventa
$$ \lim_{\Delta x \rightarrow 0} \frac{2-2}{\Delta x} = 0 $$
Quindi la derivata f'(x) è nulla per qualsiasi valore del dominio della funzione.
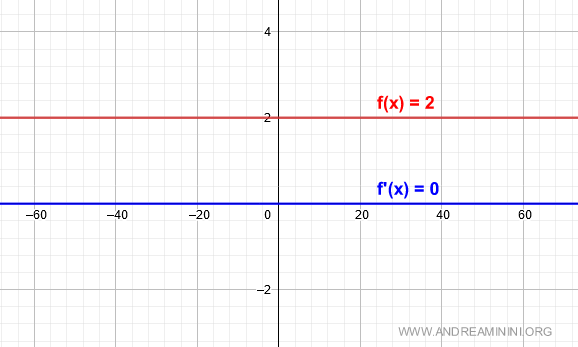
E così via.
