Il significato geometrico della derivata

Dal punto di vista geometrico, una derivata misura la pendenza del grafico di una funzione in un punto x₀ ossia il coefficiente angolare della retta tangente nel punto x₀.

L'equazione della retta tangente al grafico della funzione nel punto (x₀,f(x₀)) è la seguente:

$$ y = f(x_0) + f'(x_0) \cdot (x-x_0) $$

Dimostrazione

La funzione f(x) è definita in un intorno del punto x₀.

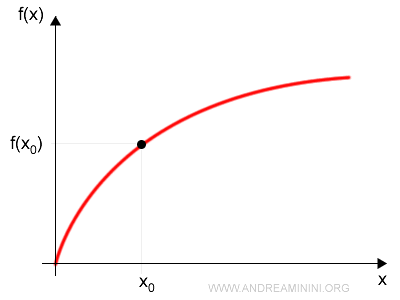
L'equazione di una retta passante per x₀ è

$$ f(x_0) = m x_0 + q $$

Nota. Le variabili m e q sono incognite. Quindi, l'equazione indica infinite rette passanti per il punto x₀ ossia il fascio di rette proprio del punto. Tra queste c'è anche la retta tangente a x₀.

Prendo un qualsiasi altro punto x del dominio della funzione.

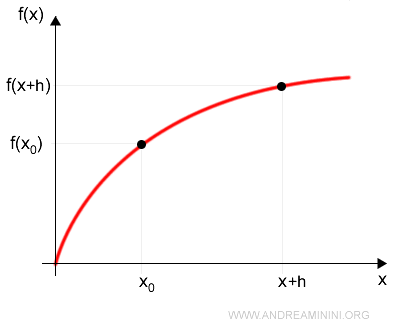
L'equazione di una retta passante per x è

$$ f(x_0+h) = m (x_0+h) + q $$

Nota. Le variabili m e q sono incognite. Pertanto, l'equazione indica infinte rette passanti per x. Anche in questo caso si tratta di un fascio di rette proprio passanti per un punto.

Pertanto, la retta secante passante per i punti x₀ e x è un sistema composto dalle due equazioni precedenti

$$ \begin{cases} f(x_0) = m x_0 + q \\ f(x_0+h) = m (x_0+h) + q \end{cases} $$

Le variabili m e q sono incognite. Per trovarle risolvo il sistema prima per m e poi per q.

In questo modo trovo l'equazione della retta secante per i punti x₀ e x.

$$ y = f(x_0) + \frac{f(x_0+h)-f(x_0)}{h} (x-x_0) $$

Nota. I passaggi algebrici per ottenerla sono i seguenti: $$ \begin{cases} f(x_0) = m x_0 + q \\ f(x_0+h) = m (x_0+h) + q \end{cases} $$ $$ \begin{cases} q= f(x_0) - m x_0 \\ f(x_0+h) = m (x_0+h) + (f(x_0) - m x_0) \end{cases} $$ $$ \begin{cases} q= f(x_0) - m x_0 \\ f(x_0+h) = m x_0+ mh + f(x_0) - m x_0 \end{cases} $$ $$ \begin{cases} q= f(x_0) - m x_0 \\ \frac{f(x_0+h) - f(x_0)}{h} = m \end{cases} $$ $$ \begin{cases} q= f(x_0) - (\frac{f(x_0+h) - f(x_0)}{h}) x_0 \\ m = \frac{f(x_0+h) - f(x_0)}{h} \end{cases} $$ Ho così trovato le incognite m e q della retta secante y=mx+q $$ y=mx+q $$ $$ y=\frac{f(x_0+h) - f(x_0)}{h} x+f(x_0) - (\frac{f(x_0+h) - f(x_0)}{h}) x_0 \ $$ $$ y=\frac{f(x_0+h) - f(x_0)}{h} (x-x_0)+f(x_0) $$

Dal punto di vista grafico la retta secante è la seguente:

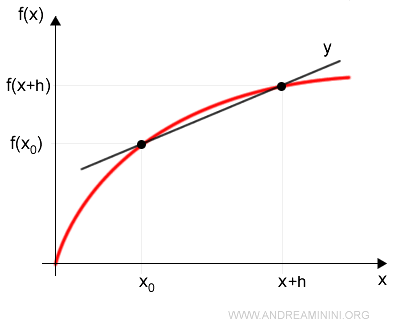
Per trovare l'equazione della retta tangente in x₀ calcolo il limite per h tendente a zero della retta secante.

$$ y_t = \lim_{h \rightarrow 0} f(x_0) + \frac{f(x_0+h)-f(x_0)}{h} (x-x_0) $$

$$ y_t =f(x_0) + \lim_{h \rightarrow 0} \frac{f(x_0+h)-f(x_0)}{h} (x-x_0) $$

$$ y_t = f(x_0) + f'(x_0) \cdot (x-x_0) $$

Ho così dimostrato che il coefficiente angolare della retta è uguale alla derivata della funzione f'(x) nel punto x₀

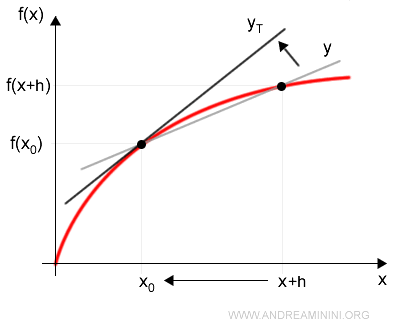
In conclusione, la derivata della funzione nel punto x₀ determina la pendenza della retta tangente nel punto x₀.

E così via.