Criterio di stretta monotonia

Funzione strettamente crescente

Una funzione continua in [a,b] e derivabile in (a,b) è strettamente crescente in [a,b] se la derivata prima f'(x)≥0 per ogni x ∈ [a,b] e la f'(x) non si annulla in nessun intervallo di [a,b]. $$\begin{cases} \forall x \in [a,b] \:\: | \:\: f'(x) \ge 0 \\ \forall (x_1,x_2) ⊂ (a,b) \:\: | \:\: f'(x)≠0 \end{cases}$$

Funzione strettamente decrescente

Una funzione continua in [a,b] e derivabile in (a,b) è strettamente decrescente in [a,b] se la derivata prima f'(x)≤0 per ogni x ∈ [a,b] e la f'(x) non si annulla in nessun intervallo di [a,b]. $$\begin{cases} \forall x \in [a,b] \:\: | \:\: f'(x) \le 0 \\ \forall (x_1,x_2) ⊂ (a,b) \:\: | \:\: f'(x)≠0 \end{cases}$$

La derivata prima della funzione strettamente crescente o decrescente può essere nulla?

La derivata di una funzione strettamente crescente o strettamente decrescente può essere nulla in un singolo punto ( es. f'(x₀)=0 ) ma non in un intervallo continuo di punti.

Un esempio pratico

Esempio 1

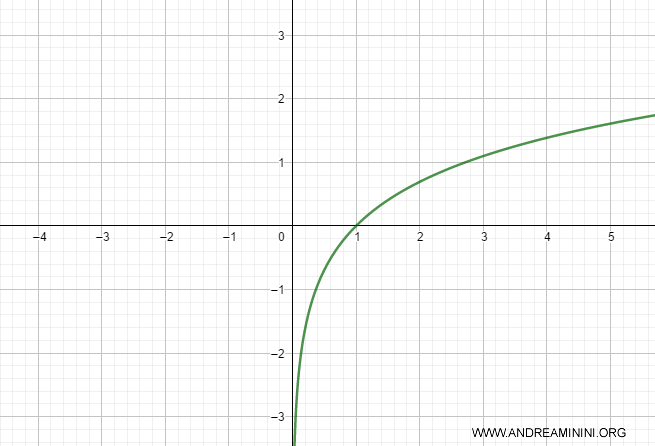
La funzione f(x)=log x è strettamente crescente nell'intervallo [0,∞] perché la derivata prima f'(x)≥0 e f'(x)≠0 in qualsiasi intervallo.

Esempio 2

La funzione f(x)=x³ è strettamente crescente nell'intervallo [0,∞] perché la derivata prima f'(x)≥0 e f'(x)≠0 in qualsiasi intervallo.

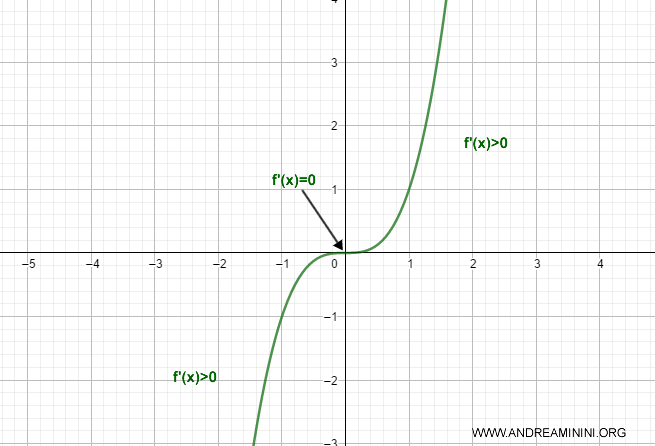
Nota. Nel punto x=0 la derivata prima della funzione è nulla f'(x)=0. La funzione è comunque strettamente crescente perché questo non viola il criterio di stretta monotonia. Secondo il criterio di stretta monotonia, la derivata prima non deve essere nulla in un intervallo.

Dimostrazione

1] A partire da una funzione f(x) con derivata f'(x)≥0 per ogni x∈[a,b] e f'(x)≠0 in ogni intervallo, devo dimostrare che la funzione è strettamente crescente.

$$\begin{cases} \forall x \in [a,b] \:\: | \:\: f'(x) \ge 0 \\ \forall (x_1,x_2) ⊂ (a,b) \:\: | \:\: f'(x)≠0 \end{cases} \Rightarrow \text{strettamente crescente}$$

Se non fosse strettamente crescente esisterebbero due punti x₁<x₂ tali che

$$f(x_1)=f(x_2)$$

Nell'intervallo (x₁,x₂) la funzione sarebbe costante secondo il criterio di monotonia.

Ma questo viola una delle ipotesi iniziali.

$$\forall x \in [x_1,x_2] \:\: | \:\: f'(x) = 0$$

Pertanto, le ipotesi iniziali implicano che la funzione sia strettamente crescente.

Nota. I due punti x₁ e x₂ non devono essere necessariamente contigui. Essendo sicuramente la f(x) una funzione crescente, in ogni punto intermedio dell'intervallo (x₁,x₂) la funzione è costante, perché non può assumere un valore superiore o inferiore. Se lo facesse non sarebbe più una funzione crescente nell'intervallo (a,b).

2] A partire dall'ipotesi di una funzione strettamente crescente, devo dimostrare che la derivata sia f'(x)≥0 per ogni x∈[a,b] e f'(x)≠0 in qualsiasi intervallo (x₁,x₂)⊂[a,b]

$$\text{strettamente crescente} \Rightarrow \begin{cases} \forall x \in [a,b] \:\: | \:\: f'(x) \ge 0 \\ \forall (x_1,x_2) ⊂ (a,b) \:\: | \:\: f'(x)≠0 \end{cases}$$

Se la derivata fosse negativa f'(x)<0 in un qualsiasi punto di [a,b] la funzione non sarebbe né una funzione crescente, né strettamente crescente.

Pertanto, la derivata deve necessariamente essere maggiore o uguale a zero in ogni punto

$$\forall x \in [a,b] \:\: | \:\: f'(x) \ge 0$$

Se la derivata prima fosse nulla f'(x)=0 in un intervallo [x₁,x₂] la funzione sarebbe costante nell'intervallo perché la funzione è crescente per ipotesi iniziale. E questo violerebbe una condizione di stretta monotonia.

Pertanto, la derivata deve essere necessariamente diversa da zero in ogni intervallo.

$$\forall (x_1,x_2) ⊂ (a,b) \:\: | \:\: f'(x)≠0$$

E così via.