Derivata sinistra

Data una funzione definita in un intorno sinistro del punto x₀, la funzione f(x) è derivabile da sinistra in x₀ se esiste ed è finito il limite sinistro del rapporto incrementale tra x₀ e x per x tendente a x₀. $$ f'_-(x_0) = \lim_{x \rightarrow x_0^-} \frac{f(x)-f(x_0)}{x-x_0} $$ poiché Δx=x-x₀ si può scrivere anche $$ f'_-(x_0) = \lim_{Δx \rightarrow 0^-} \frac{f(x_0+Δx)-f(x_0)}{Δx} $$ detta derivata sinistra di f(x)

In questo caso prendo in considerazione soltanto l'intorno sinistro del punto x₀.

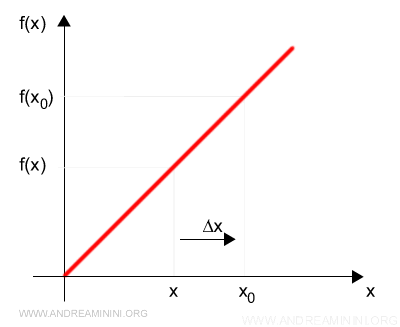
Nel calcolo della derivata sinistra la differenza Δx=x-x₀ è sempre negativa.

$$ x - x_0 < 0 $$

Quindi

$$ Δx<0 $$

Nota. La notazione cambia a seconda degli autori. A volte il punto x è sostituito da x₀-δ. Il concetto è comunqe sempre lo stesso. Si tratta di un punto a sinistra di x₀ che converge a x₀.

 

L'intorno a destra del punto x₀ non si considera.

Un esempio pratico

Verifico se esiste la derivata sinistra della funzione f(x)=|x| nel punto x₀=2.

$$ f(x) = 2 $$

Calcolo il limite nell'intorno sinistro del punto x₀

$$ f'_-(x_0) = \lim_{x \rightarrow x_0^-} \frac{f(x)-f(x_0)}{x-x_0} $$

poiché x₀=2

$$ f'_-(2) = \lim_{x \rightarrow 2^-} \frac{f(x)-f(2)}{x-2} $$

$$ f'_-(2) = \lim_{x \rightarrow 2^-} \frac{|x|-|2|}{x-2} $$

$$ f'_-(2) = \lim_{x \rightarrow 2^-} \frac{x-2}{x-2} = +1 $$

In questo caso la x del limite tende al valore 2^- da sinistra senza mai raggiungerlo ( es. 1.999999 ).

$$ f'_-(2) = \lim_{x \rightarrow 2^-} \frac{x-2}{x-2} = \lim_{x \rightarrow 2^-} \frac{1.99999-2}{1.99999-2} $$

Quindi, la differenza x-2 è sempre negativa sia al numeratore che al denominatore.

$$ f'_-(2) = \lim_{x \rightarrow 2^-} \frac{1.99999-2}{1.99999-2} = \lim_{x \rightarrow 2^-} \frac{-0.000001}{-0.000001} $$

 

Pertanto, il quoziente è sempre positivo.

I valori al numeratore e al denominatore del rapporto sono uguali e si può semplificare con +1.

$$ f'_-(2) = \lim_{x \rightarrow 2^-} \frac{-0.000001}{-0.000001} = \lim_{x \rightarrow 2^-} 1 = +1 $$

In conclusione, la derivata sinistra della funzione f(x) nel punto x₀=2 è +1.

$$ f'_-(2) = +1 $$

Nota. Posso ottenere lo stesso risultato anche usando l'altra forma del limite sinistro. $$ f'_-(x_0) = \lim_{Δx \rightarrow 0^-} \frac{f(x_0+Δx)-f(x_0)}{Δx} $$ $$ f'_-(2) = \lim_{Δx \rightarrow 0^-} \frac{f(2+Δx)-f(2)}{Δx} $$ $$ f'_-(2) = \lim_{Δx \rightarrow 0^-} \frac{|2+Δx|-|2|}{Δx} $$ Nel limite di sinistra il valore Δx=x-x₀ è sempre negativo Δx<0. Quindi, posso riscrivere la formula in $$ f'_-(2) = \lim_{Δx \rightarrow 0^-} \frac{|2-Δx|-|2|}{-Δx} $$ La differenza al numeratore |2-Δx|-|2| è sempre negativa. Quindi, anche in questo caso sia il numeratore che il denominatore sono numeri negativi. Pertanto il quoziente è positivo. $$ f'_-(2) = \lim_{Δx \rightarrow 0^-} \frac{-Δx}{-Δx} =\lim_{Δx \rightarrow 0^-} 1 = +1 $$ Il risultato è sempre lo stesso.

E così via.