Formula di Taylor
La formula di Taylor approssima il comportamento di una funzione f(x) derivabile n volte nell'intorno di un punto x0 di R, mediante dei polinomi di grado n a cui si aggiunge un resto R. $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x-x_0)^k + R_n(x) $$ con $$ \lim_{x \rightarrow x_0} \frac{R_n}{(x-x_0)^n} = 0 $$
Il polinomio è detto Polinomio di Talyor di f(x) in x0 di grado/ordine n.
Quanto più alto è il grado n del polinomio, tanto più accurata sarà l'approssimazione della funzione.
Pertanto, il resto R del polinomio è nullo per n tendente a infinito.
$$ \lim_{n \rightarrow ∞} R_n = 0 $$
A cosa serve? La formula di Taylor mi permette di trasformare una funzione f(x) in un polinomio algebrico P. In quest'ultima forma è più semplice e immediato studiare le sue caratteristiche.
Un esempio di calcolo
Ho la funzione esponenziale
$$ f(x) = e^x $$
Prendo come riferimento il punto x0=0.
$$ x_0 = 0 $$
dove la funzione è uguale a 1
$$ f(0) = e^0 = 1 $$
Poiché tutte le derivate della funzione coincidono con ex
$$ D[e^x] = e^x $$
per ogni grado k ho
$$ f^{(k)}(0)=1 $$
Pertanto, lo sviluppo polinomiale della funzione di grado n=2 è
$$ f(x) = \frac{f^{(0)}(x_0)}{0!} \cdot (x-x_0)^0 + \frac{f^{(1)}(x_0)}{1!} \cdot (x-x_0)^1 + \frac{f^{(2)}(x_0)}{2!} \cdot (x-x_0)^2 + R_2 $$
$$ f(x) = \frac{D^{(0)}[e(x_0)]}{0!} \cdot (x-x_0)^0 + \frac{D^{(1)}[e(x_0)]}{1!} \cdot (x-x_0)^1+ \frac{D^{(2)}[e(x_0)]}{2!} \cdot (x-x_0)^2 + R_2 $$
Considerando che la derivata zero è la funzione stessa.
$$ f(x) = \frac{e(x_0)}{0!} \cdot (x-x_0)^0 + \frac{D^{(1)}[e(x_0)]}{1!} \cdot (x-x_0)^1+ \frac{D^{(2)}[e(x_0)]}{2!} \cdot (x-x_0)^2 + R_2 $$
Sostituisco x0=0
$$ f(x) = \frac{e(0)}{0!} \cdot (x-0)^0 + \frac{D^{(1)}[e(0)]}{1!} \cdot (x-0)^1+ \frac{D^{(2)}[e(0)]}{2!} \cdot (x-0)^2 + R_2 $$
$$ f(x) = \frac{e(0)}{0!} \cdot x^0 + \frac{D^{(1)}[e(0)]}{1!} \cdot x^1+ \frac{D^{(2)}[e(0)]}{2!} \cdot x^2 + R_2 $$
Sapendo che ogni derivata k-esima di ex è sempre ex
$$ f(x) = \frac{e(0)}{0!} \cdot x^0 + \frac{e(0)}{1!} \cdot x^1+ \frac{e(0)}{2!} \cdot x^2 + R_2 $$
Poiché e0=1
$$ f(x) = \frac{1}{0!} \cdot x^0 + \frac{1}{1!} \cdot x^1+ \frac{1}{2!} \cdot x^2 + R_2 $$
Calcolo i fattoriali al denominatore.
Il fattoriale di 0! è per convenzione uguale a 1.
$$ f(x) = \frac{1}{1} \cdot x^0 + \frac{1}{1} \cdot x^1+ \frac{1}{2} \cdot x^2 + R_2 $$
$$ f(x) = \frac{x^0}{1} + \frac{x^1}{1} + \frac{x^2}{2} + R_2 $$
$$ f(x) = 1 + x + \frac{x^2}{2} + R_2 $$
Pur essendo un polinomio di Taylor di grado molto basso, il polinomio approssima abbastanza bene la funzione f(x)=ex
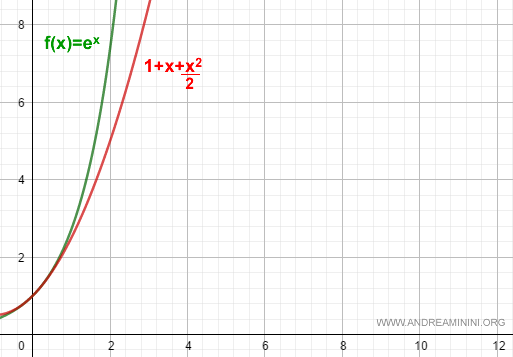
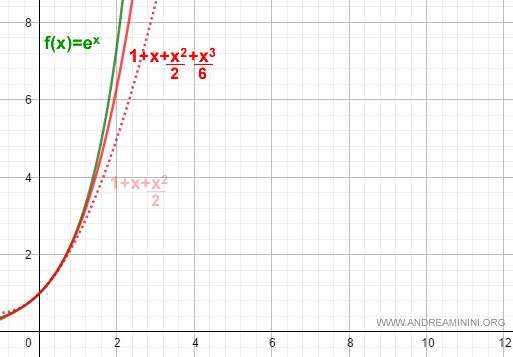
Se aumentassi il grado del polinomio a k+1=3 otterrei una migliore approssimazione.
$$ f(x) = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + R_3 $$
Il nuovo polinomio di grado 3 è più vicino al grafico della funzione rispetto al precedente polinomio di grado 2 ( punteggiato ).
Pertanto, il limite del resto del polinomio per k tendente a infinito è zero.
$$ \lim_{k \rightarrow ∞} R_k = 0 $$
La dimostrazione
Suppongo che la derivata f(n)(x) sia continua in x0.
Devo dimostrare che il resto della formula di Taylor tende a zero per x tendente a x0.
$$ \lim_{x \rightarrow x_0} \frac{R_n}{(x-x_0)^n} = 0 $$
Sapendo che R è uguale alla differenza tra la funzione f(x) e il polinomio di Taylor
$$ R_n = f(x) - P(x) $$
$$ R_n = f(x) - [ f(x_0) + f'(x_0)(x-x_0)+...+\frac{f^{(n)}(x_0)(x-x_0)^n}{n!} ] $$
Sostituisco R nel limite.
Il risultato è una forma indeterminata 0/0.
$$ \lim_{x \rightarrow x_0} \frac{f(x) - [ f(x_0) + f'(x_0)(x-x_0)+...+\frac{f^{(n)}(x_0)(x-x_0)^n}{n!} ] }{(x-x_0)^n} = \frac{0}{0} $$
Nota. Al numeratore la differenza tra la funzione f(x) e il polinomio di Taylor è nulla perché nel punto x0 sono coincidenti. Al denominatore la differenza x-x0 è ovviamente nulla per x→x0. Questo spiega perché il limite è una forma indeterminata 0/0.
Per risolvere la forma indeterminata 0/0 applico il teorema di L'Hopital.
Calcolo la derivata per x del numeratore e del denominatore.
$$ \lim_{x \rightarrow x_0} \frac{ D [ f(x) - [ f(x_0) + f'(x_0)(x-x_0)+...+\frac{f^{(n)}(x_0)(x-x_0)^n}{n!} ] ] }{ D[ (x-x_0)^n ] } $$
$$ \lim_{x \rightarrow x_0} \frac{ f'(x) - [ f'(x_0) + f"(x_0)(x-x_0) +...+ \frac{f^{(n)}(x_0) \cdot (x-x_0)^{n-1} }{(n-1)!} ] } { n \cdot (x-x_0)^{n-1} } = \frac{0}{0} $$
Essendo ancora una forma indeterminata 0/0, applico di nuovo il teorema di L'Hopital per n volte.
Dopo n derivazioni del numeratore e del denominatore ottengo:
$$ \lim_{x \rightarrow x_0} \frac{f^{(n)}(x)-f^{(n)}(x_0)}{n!} $$
Poiché la funzione f(x) è continua in x0 allora il numeratore è zero perché f(x0)-f(x)=0 con x→x0.
Il denominatore è, invece, una costante n! pari al fattoriale del grado n del polinomio di Taylor.
Pertanto, il limite è nullo.
$$ \lim_{x \rightarrow x_0} \frac{f^{(n)}(x)-f^{(n)}(x_0)}{n!} = 0 $$
Quindi anche il limite iniziale è nullo
$$ \lim_{x \rightarrow x_0} \frac{ f'(x) - [ f'(x_0) + f"(x_0)(x-x_0) +...+ \frac{f^{(n)}(x_0) \cdot (x-x_0)^{n-1} }{(n-1)!} ] } { n \cdot (x-x_0)^{n-1} } = 0 $$
ossia
$$ \lim_{x \rightarrow x_0} \frac{R_n}{(x-x_0)^n} = 0 $$
E questo completa la dimostrazione della formula di Taylor.
Il resto di Peano
Il resto di Peano è la differenza tra il polinomio pn di ordine n e centro x0 realizzato con la formula di Taylor e la funzione f(x) che si vuole approssimare. $$ R_n(x) = f(x)-p_n(x) $$
Il resto di Peano misura l'errore quando approssimo la funzione f(x) con il polinomio di Taylor.
$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x-x_0)^k + R_n(x) $$
Il polinomio di Talyor pn(x) è
$$ p_n(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x-x_0)^k $$
Quindi, con un semplice passaggio algebrico.
$$ f(x) = p_n(x) + R_n(x) $$
$$ f(x) - p_n(x) = R_n(x) $$
Il resto di Peano R è la differenza tra la funzione f(x) e il polinomio di Taylor pn(x) di ordine n centrato su x0.
Il resto di Peano Rn(x) è un infinitesimo in x0 di ordine superiore a (x-x0)n se la funzione f(x) è derivabile n volte in x0. $$ \lim_{x \rightarrow x_0} \frac{R_n(x)}{(x-x_0)^n}=0 $$
La dimostrazione
$$ \lim_{x \rightarrow x_0} \frac{R_n(x)}{(x-x_0)^n} $$
Sapendo che Rn(x)=f(x)-pn(x)
$$ \lim_{x \rightarrow x_0} \frac{f(x) - p_n(x)}{(x-x_0)^n} $$
Sostituisco pn(x) con il polinomio di Taylor.
$$ \lim_{x \rightarrow x_0} \frac{f(x) - [ f(x_0) + f'(x_0)(x-x_0) + ... + \frac{f^{(n)}(x_0)(x-x_0)^n}{n!} ] }{(x-x_0)^n} $$
Il limite precedente è una forma indeterminata del tipo 0/0.
Per risolverlo applico il teorema di De L'Hopital per n-1 volte.
$$ \lim_{x \rightarrow x_0} \frac{f^{(n-1)}(x) - [ f^{(n-1)}(x_0) + f^{(n)}(x_0)(x-x_0) ] }{ n! (x-x_0)} $$
Sposto 1/n! fuori dal limite
$$ \frac{1}{n!} \lim_{x \rightarrow x_0} \frac{f^{(n-1)}(x) - [ f^{(n-1)}(x_0) + f^{(n)}(x_0)(x-x_0) ] }{ (x-x_0)} $$
$$ \frac{1}{n!} \lim_{x \rightarrow x_0} \frac{f^{(n-1)}(x) - f^{(n-1)}(x_0) - f^{(n)}(x_0)(x-x_0) }{ (x-x_0)} $$
Scorporo l'ultimo termine dalla frazione e semplifico
$$ \frac{1}{n!} \lim_{x \rightarrow x_0} [ \frac{f^{(n-1)}(x) - f^{(n-1)}(x_0) }{ (x-x_0)} - \frac{f^{(n)}(x_0)(x-x_0) }{ (x-x_0)} ] $$
$$ \frac{1}{n!} \lim_{x \rightarrow x_0} [ \frac{f^{(n-1)}(x) - f^{(n-1)}(x_0) }{ (x-x_0)} - f^{(n)}(x_0) ] $$
Scorporo i limiti
$$ \frac{1}{n!} [ \lim_{x \rightarrow x_0} \frac{f^{(n-1)}(x) - f^{(n-1)}(x_0) }{ (x-x_0)} - \lim_{x \rightarrow x_0} f^{(n)}(x_0) ] $$
Applico il teorema di De L'Hopital sul primo limite che diventa f(n)(x).
$$ \frac{1}{n!} \cdot [ f^{(n)}(x_0) - \lim_{x \rightarrow x_0} f^{(n)}(x_0) ] $$
Il secondo limite è f(n)(x).
$$ \frac{1}{n!} \cdot [ f^{(n)}(x_0) - f^{(n)}(x_0) ] $$
$$ \frac{1}{n!} \cdot [ 0 ] $$
$$ = 0 $$
Nota. Il resto di Peano Rn(x) è un infinitesimo di ordine superiore rispetto a (x-x0)n. $$ \lim_{x \rightarrow x_0} \frac{R_n(x)}{(x-x_0)^n}=0 $$ Quindi, nel polinomio di Taylor posso indicarlo anche con il simbolo "o piccolo". $$ R_n(x)=o((x-x_0)^n) $$ ossia . $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x-x_0)^k + o((x-x_0)^n) $$
La formula di Taylor in una notazione alternativa
Se il resto di Peano è un "o piccolo" di (x-x0)n posso riscrivere la formula di Taylor anche in questa forma alternativa
$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x-x_0)^k + o((x-x_0)^n) $$
La stima del resto di Peano
Data una funzione f(x) derivabile n+1 volte in un intorno di x0 con derivata continua, se M è il massimo valore della funzione nell'intorno, una stima del resto di Peano è la seguente $$ |R_n(x)| \le M \cdot \frac{|x-x_0|^{n+1}}{(n+1)!} $$
La formula di Mac Laurin
La formula di Mac Laurin è un caso particolare della formula di Taylor, quando x0=0 è uguale a zero. $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!} \cdot (x)^k + o((x)^n) $$
E così via.
- La formula di Taylor
- La formula di Mac Laurin
- Il resto di Lagrange
- La serie di Taylor
- La serie di Fourier
Esercizi
- Come calcolare il polinomio di Taylor del seno
- Come calcolare i limiti indefiniti con il polinomio di Taylor
