Rapporto incrementale della funzione
La definizione di rapporto incrementale
Il rapporto incrementale di una funzione è $$ \frac{f(x+h)-f(x)}{h} $$
Il valore h è l'incremento della variabile indipendente.
La spiegazione
Ho una funzione f(x) definita in un intervallo (a,b).
$$ f(x) $$
Per rendere più semplice la spiegazione rappresento la funzione f(x) sul diagramma cartesiano
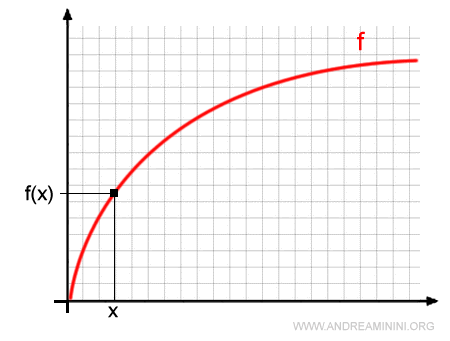
Prendo un generico numero h compreso nell'intervallo (a,b) come incremento della variabile indipendente x.
Ora la funzione f(x) assume un nuovo valore.
$$ f(x+h) $$
Rappresento la variazione sul diagramma cartesiano
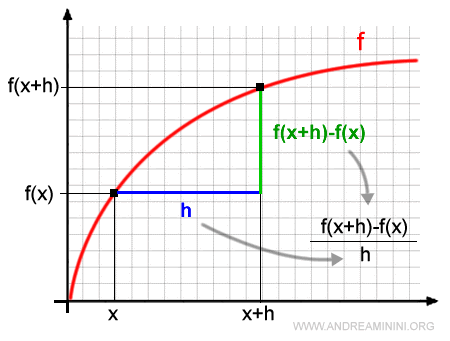
L'incremento del valore della variabile dipendente, ossia della funzione f(x) è
$$ f(x+h)-f(x) $$
Il rapporto tra l'incremento della variabile dipendente e quello della variabile indipendente è detto rapporto incrementale.
$$ \frac{f(x+h)-f(x)}{h} $$
Nota. Il rapporto incrementale della funzione f(x) è definito per qualsiasi valore di h nell'intervallo (a,b) tranne che per h=0. Quando il denominatore del rapporto è nullo (h=0) si ha una divisione per zero ossia un'operazione matematica indefinita.
