La derivata e il coefficiente angolare
Il concetto geometrico di derivata di una funzione f(x) è strettamente legato al coefficiente angolare della retta tangente in un punto della funzione. $$ f'(x_0) = tan \:\: α $$ dove α è il coefficiente angolare della retta tangente nel punto f(x0)
La dimostrazione e spiegazione
Prendo come riferimento due punti A e B del grafico della funzione
$$ f(x) $$
$$ f(x+h) $$
Dove h è l'incremento della variabile indipendente x.
La distanza tra i due punti è
$$ f(x+h) - f(x) $$
Poi individuo un punto C dall'intersezione delle rette parallele agli assi passanti per A e B.
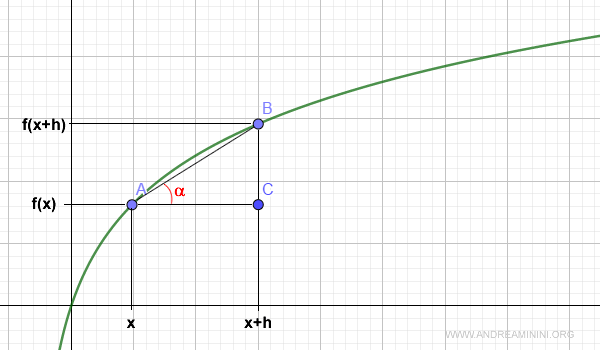
Unendo i tre punti A, B, C ottengo un triangolo rettangolo dove i cateti sono:
- AC = h ossia Δx
- BC = f(x+h)-f(x) ossia Δy
Il rapporto incrementale della funzione in questi due punti è
$$ \frac{f(x+h)-f(x)}{h} $$
Equivale al coefficiente angolare tan α.
$$ tan \:\: α = \frac{f(x+h)-f(x)}{h} $$
Perché è uguale alla tangente? Ponendo AB=1 (raggio unitario) in trigonometria il rapporto incrementale BC/AC equivale al rapporto tra seno e coseno.
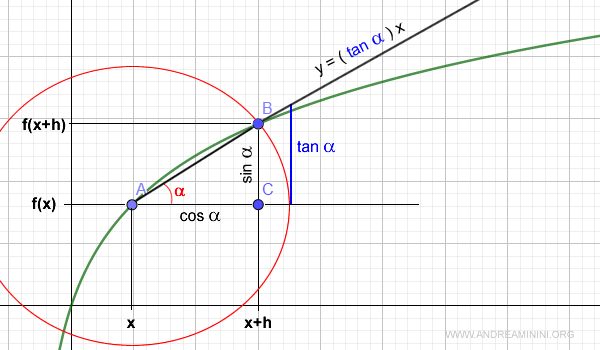
A sua volta, il rapporto tra seno e coseno è uguale alla tangente. $$ \frac{BC}{AC} = \frac{sin \:α}{cos \:α} = tan \:α $$
Il rapporto incrementale della funzione ( tan α ) è anche uguale al coefficiente angolare della retta AB.
Esempio. Se AC = 6 e BC =4, il rapporto incrementale è uguale a BC/AC ossia 4/6 = 2/3. Quindi la tangente dell'angolo α è uguale a 2/3.
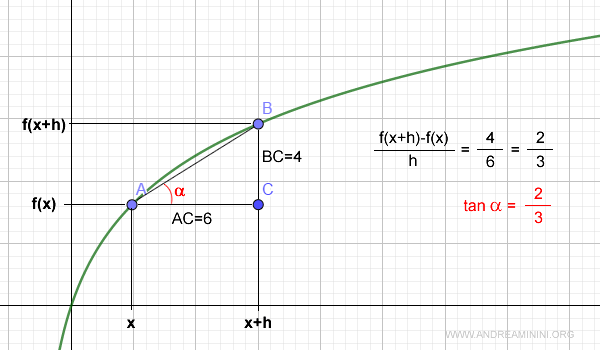
Tan α è anche il coefficiente angolare di una retta passante per i punti A e B. Quindi il segmento AB è parallelo a una generica retta y = ( tan α ) x passante per l'origine dove alfa è il coefficiente angolare ossia y = 2/3 x.
Se la funzione è derivabile nel punto x, posso calcolare il limite del rapporto incrementale per h tendente a zero.
Ottengo così la derivata di f(x) nel punto x.
$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} = f'(x) $$
Il limite del rapporto incrementale ( ossia la derivata ) ha anche un altro importante significato.
E' uguale al coefficiente angolare β della tangente alla funzione del punto x.
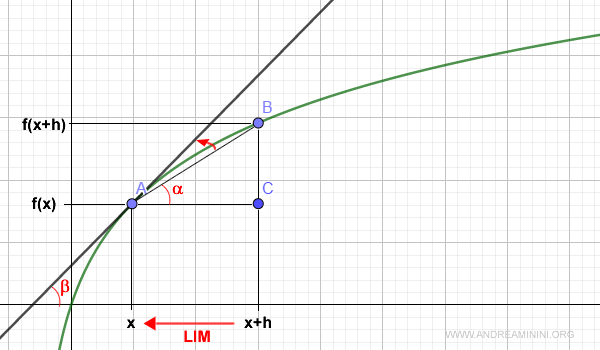
Pertanto l'equazione cartesiana della retta tangente è la seguente:
$$ y = β \cdot x $$
In generale posso affermare che
Dato un punto (x0,y0) della funzione l'equazione della retta tangente alla funzione nel punto x0 è la seguente $$ y-y_0= f'(x_0) \cdot (x - x_0 ) $$
Questa formula mi permette di ottenere l'equazione della tangente nel punto (x0,y0), fatta eccezione per il caso in cui la tangente sia verticale.
Per verificare se nel punto esiste una tangente verticale occorre seguire un'altra strada.
Nota. In un punto x0 in cui la funzione è continua, esiste una retta tangente verticale se il limite della funzione in x0 esiste ed è uguale a +∞ oppure a -∞.
Un esempio semplice
Prendo come esempio la funzione x2
$$ f(x) = x^2 $$
Fisso un punto x = 1 e un incremento h=1
$$ f(x) = f(1) = 1 $$
$$ f(x+h) = f(1+1) = f(2) = 4 $$
Ottengo così due punti A e B.
$$ A \begin{pmatrix} 1 \\ 1 \end{pmatrix}$$
$$ B \begin{pmatrix} 2 \\ 4 \end{pmatrix}$$
Poi individuo un punto C.
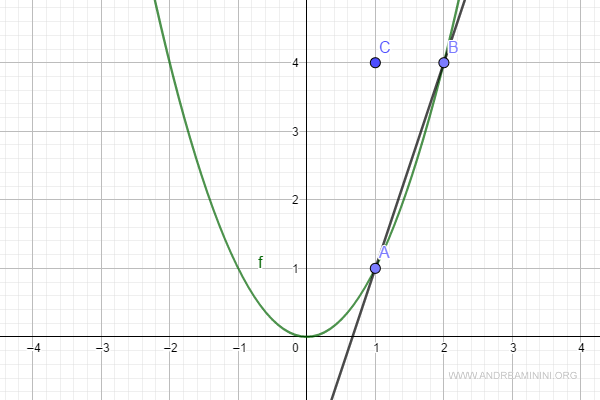
Ora posso calcolare il rapporto incrementale della funzione.
$$ \frac{f(x+h)-f(x)}{h} = \frac{4-1}{1} = 3 $$
Il rapporto incrementale è uguale a 3.
Pertanto, la tangente dell'angolo alfa è uguale a 3.
$$ tan \: α = 3 $$
E quindi anche il coefficiente angolare (m) della retta AB è uguale a 3.
Per trovare l'equazione cartesiana passante per i punti A e B uso la seguente formula:
$$ y-y_0= m \cdot (x - x_0 ) $$
Il coefficiente angolare lo conosco (m=3).
$$ y-y_0= 3 \cdot (x - x_0 ) $$
Prendo il punto A (1,1) come punto di riferimento della retta (x0,y0).
$$ y-1= 3 \cdot (x - 1 ) $$
$$ y= 3 \cdot x - 3 +1 $$
$$ y= 3 \cdot x - 2 $$
Ho così individuato l'equazione cartesiana della retta passante per i punti A e B.
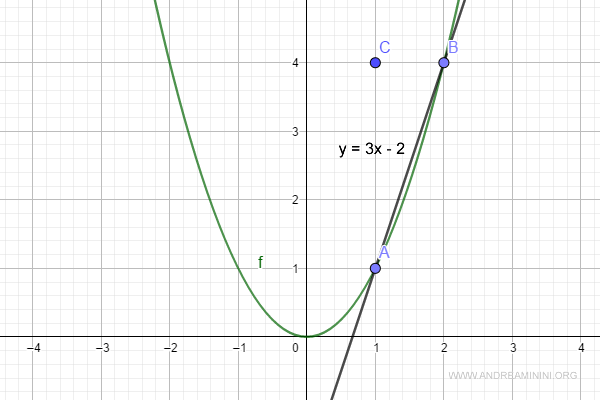
A questo punto calcolo il limite del rapporto incrementale per h tendente a zero.
$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} = f'(x) $$
Il valore del limite è la derivata prima f'(x) della funzione f(x).
E' anche il valore della tangente dell'angolo α , ossia il coefficiente angolare della retta (r) tangente al punto A della funzione f(x).
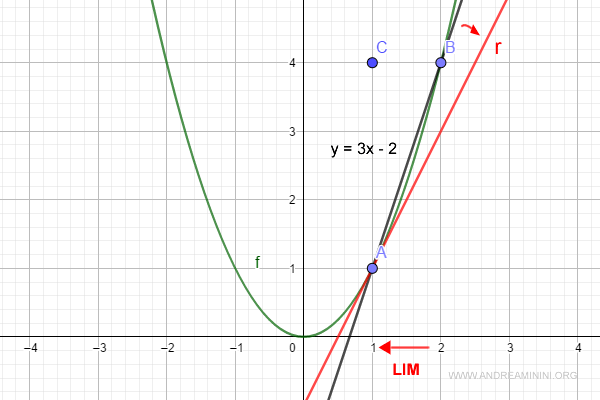
Qual è l'equazione della retta tangente?
In questo caso non ci sono due punti ma solo uno.
Tuttavia, so già che il limite del rapporto incrementale è uguale a tan α e alla derivata prima di f'(x).
$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} = tan \:\: α = f'(x) $$
Quindi, per trovare il coefficiente angolare della retta tangente mi basta conoscere la funzione derivata f'(x).
La derivata di f(x)=x2 è uguale a f'(x)=2x.
$$ f'(x) = 2x $$
E nel punto x=1 la derivata f'(x) è uguale a 2.
Quindi anche il coefficiente angolare della retta tangente al punto A è uguale a 2.
$$ f'(1) = 2 \cdot 1 = 2 $$
Ora, per trovare l'equazione cartesiana passante per i punti A e B uso la seguente formula:
$$ y-y_0= m \cdot (x - x_0 ) $$
Il coefficiente angolare lo conosco (m=2).
$$ y-y_0= 2 \cdot (x - x_0 ) $$
Prendo il punto A (1,1) come punto di riferimento della retta (x0,y0).
$$ y-1= 2 \cdot (x - 1 ) $$
$$ y= 2 \cdot x - 2 +1 $$
$$ y= 2 \cdot x - 1 $$
Ho così individuato l'equazione cartesiana della retta tangente al punto A della funzione f(x).
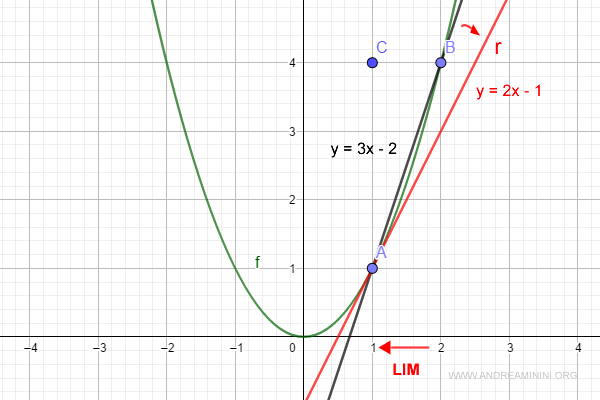
E per calcolare la retta tangente in un altro punto?
Il procedimento è sempre lo stesso.
Calcolo il coefficiente angolare della retta nel nuovo punto.
Poi costruisco l'equazione cartesiana della retta usando le coordinate del nuovo punto.
Esempio: la retta tangente al punto B
La retta r' è tangente al punto B ( blu ).
Ha un coefficiente angolare diverso dalla retta tangente al punto A ( rossa ). L'inclinazione è differente.
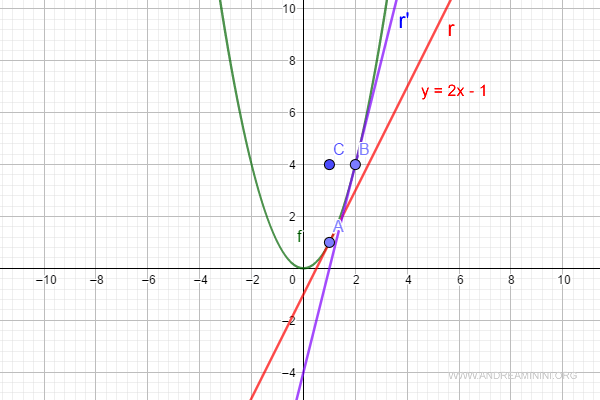
La derivata prima f'(x) è sempre la stessa ma il valore del dominio (x=2) è differente.
Il coefficiente angolare della retta r' è uguale a 4.
$$ f'(x) = 2 \cdot x = tan \: α $$
$$ f'(2) = 2 \cdot 2 = 4 $$
Una volta trovato il coefficiente angolare ( m = 4 ), calcolo l'equazione cartesiana della retta r' usando la solita formula.
$$ y-y_0= m \cdot (x - x_0 ) $$
$$ y-y_0= 4 \cdot (x - x_0 ) $$
In questo caso il punto di riferimento è B ( 2, 4 ).
$$ y-4= 4 \cdot (x - 2 ) $$
$$ y= 4 \cdot x - 8 + 4 $$
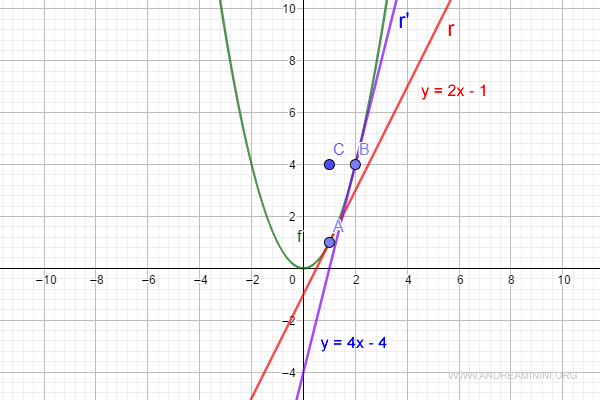
$$ y= 4 \cdot x - 4 $$
Ho così trovato l'equazione cartesiana retta tangente al punto B ( blu ).
E così via.
