Il teorema di Fermat
Se una funzione f(x) definita in un intervallo [a,b] ha un punto di massimo o di minimo relativo nel punto x0, allora la derivata prima della funzione f'(x0) è nulla. $$ f'(x_0)=0 $$
- E' un minimo relativo se nell'intorno di x0 la derivata sinistra è negativa e la derivata destra è positiva. $$ f'_-(x_0) < 0 \:\:\:, \:\:\: f'_+(x_0) > 0 $$
- E' un massimo relativo se nell'intorno di x0 la derivata sinistra è positiva e la derivata destra è negativa. $$ f'_-(x_0) > 0 \:\:\:, \:\:\: f'_+(x_0) < 0 $$
Nota. Il teorema di Fermat ha però un limite. Lo posso applicare soltanto se il punto x0 è un punto interno dell'intervallo [a,b]. Non potrei usarlo se x0 è uno degli estremi dell'intervallo (a oppure b) perché in questi punti non è possibile calcolare la derivata.
Un esempio pratico
Studio la funzione f(x) nell'intervallo dei numeri reali
$$ f(x)=x^2 $$
La derivata prima della funzione è
$$ f'(x)=2x $$
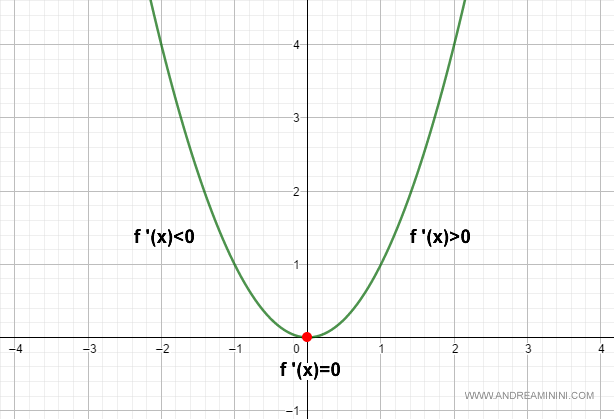
La funzione derivata prima è uguale a zero soltanto nel punto x=0.
$$ f'(0)=0 $$
Quindi, nel punto x=0 la funzione registra sicuramente un massimo o minimo relativo.
E' un minimo o un massimo?
Per capire se è un minimo o un massimo analizzo la derivata sinistra e destra nell'intorno di x0=0.
$$ f'_-(0) < 0 $$
$$ f'_+(0) > 0 $$
In questo caso, essendo decrescente a sinistra (derivata negativa) e crescente a destra (derivata positiva), il punto x0 è un minimo relativo.
Nota. In alternativa, se la funzione è derivabile due volte, è possibile studiare il segno della derivata seconda. Se la derivata seconda è maggiore-uguale a zero è un minimo, se è minore-uguale a zero è un massimo.
Dimostrazione
Se una funzione definita in [a,b] ha un punto di massimo in x0, allora la funzione è crescente a sinistra di x0 e decrescente a destra di x0.
Questo equivale a dire che la derivata prima nell'intorno di x0 è positiva a sinistra e negativa a destra di x0.
$$ f'_-(x_0) = \lim_{h \rightarrow 0^-} \frac{f(x_0+h)-f(x_0)}{h} \ge 0 $$
$$ f'_+(x_0) = \lim_{h \rightarrow 0^+} \frac{f(x_0+h)-f(x_0)}{h} \le 0 $$
Secondo le condizioni di derivabilità in un punto, la funzione è derivabile nel punto x0 se la derivata prima f'(x0) è uguale alla derivata sinistra e destra di x0.
Pertanto, la derivata in x0 è necessariamente uguale a zero, perché è l'unico punto in comune tra la derivata destra e la derivata sinistra.
$$ f'(x_0) = \lim_{h \rightarrow 0} \frac{f(x_0+h)-f(x_0)}{h} = 0 $$
Nota. Un ragionamento analogo si può fare per dimostrare il punto di minimo. In questo caso la funzione f(x) è decrescente a sinistra (derivata sinistra negativa) e crescente a destra (derivata destra positiva) del punto x0. Se la funzione è derivabile in x0, la derivata prima può essere soltanto uguale a zero perché deve uguagliare la derivata sinistra e destra.
Minimi e massimi agli estremi
Per capire se un punto estremo di un intervallo è un massimo o un minimo relativo, calcolo la derivata destra/sinistra e analizzo l'intorno del punto. E' un massimo se $$ f'(x_0) \cdot (x-x_0) \le 0 $$ E' un minimo se $$ f'(x_0) \cdot (x-x_0) \ge 0 $$
Esempio
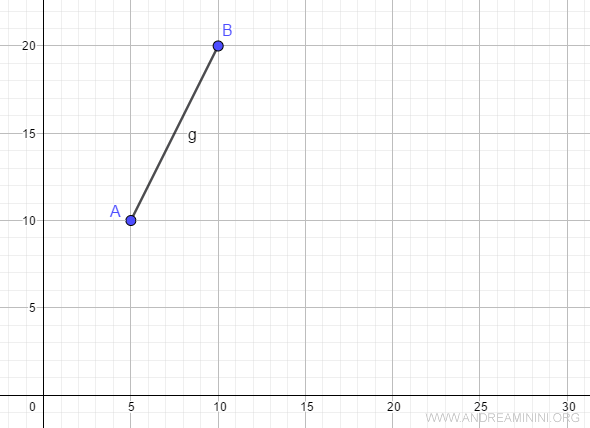
Ho la funzione f(x) definita nell'intervallo [5,10]
$$ f(x)=2x $$
Verifico se x=10 (estremo destro B) è un massimo relativo.
La derivata destra di f(10) non esiste perché x=10 è l'estremo destro dell'intervallo.
La derivata sinistra di f(10) invece esiste ed è uguale a
$$ f'_-(10)=2 $$
Applico la formula per studiare il comportamento della funzione nell'intervallo
$$ f'(x_0) \cdot (x-x_0) $$
$$ 2 \cdot (x-10) $$
Noto subito che per qualsiasi x compreso nell'intervallo [5,10] l'equazione è minore o uguale a zero, perché la componente (x-10) è negativa (o nulla nel caso di x=10).
$$ 2 \cdot (x-10) \le 0 $$
Pertanto, il punto x=10 è un massimo relativo.
Nota. Lo stesso metodo posso applicarlo per studiare l'estremo B e verificare che si tratta di un minimo relativo. La formula è applicabile anche nei punti intermedi dell'intervallo e non solo agli estremi. Ad esempio, ho la funzione è f(x)=sin x definita nell'intervallo [1,2]. La derivata è f'(x)=cos x. Devo capire se il punto x=π/2 è un minimo, un massimo oppure nessuna delle due.
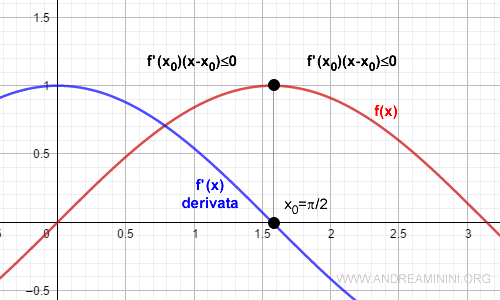
Analizzo l'intorno del punto x=π/2. A sinistra la derivata sinistra f'-(x0)>0 e (x-x0)<0. A destra la derivata destra f'+(x0)<0 e (x-x0)>0. In entrambi i casi, sia a sinistra che a destra, nell'intorno di x0=π/2 la formula è sempre minore-uguale a zero $$ f'(x_0) \cdot (x-x_0) \le 0 $$ Pertanto x=π/2 è un punto di massimo relativo della funzione f(x)=sin x.
E così via.
