La derivata di una funzione lineare
Definizione
La derivata di una funzione lineare f(x)=mx+n è il coefficiente m. $$ f(x)=mx+n \:\: \rightarrow \:\: f'(x)=m $$
La spiegazione è facilmente dimostrabile.
Dimostrazione
Data una funzione lineare f(x) nell'intervallo (a,b) e un punto qualsiasi x del suo dominio.
$$ f(x) = mx + n $$
Calcolo la derivata prima della funzione f'(x) tramite il limite del rapporto incrementale per h tendente a zero.
$$ f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} $$
Sapendo che
- f(x) = mx+n
- f(x+h) = m(x+h)+n
Li sostituisco nel rapporto incrementale
$$ \lim_{h \rightarrow 0} \frac{m(x+h)+n - (mx+h)}{h} $$
$$ \lim_{h \rightarrow 0} \frac{mx+mh+n-mx-n}{h} $$
$$ \lim_{h \rightarrow 0} \frac{mh}{h} $$
$$ \lim_{h \rightarrow 0} m = m $$
Ho così dimostrato che la derivata della funzione lineare è uguale al coefficiente m.
Un esempio pratico
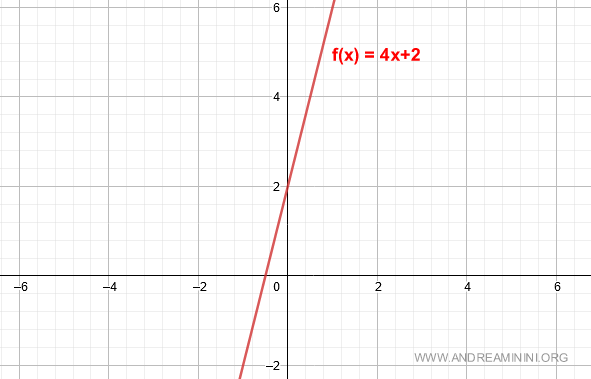
Ho la seguente funzione lineare
$$ f(x) = 4x + 2 $$
Il grafico della funzione è il seguente:
Calcolo la derivata di f(x) tramite il limite del rapporto incrementale in un punto qualsiasi x.
$$ f'(x)= \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} $$
Sapendo che
- f(x) = 4x+2
- f(x+h) = 4(x+h)+2
Li sostituisco nel rapporto incrementale
$$ f'(x)= \lim_{h \rightarrow 0} \frac{4(x+h)+2 - (4x+2)}{h} $$
$$ f'(x)= \lim_{h \rightarrow 0} \frac{4x+4h+2 -4x-2}{h} = 4 $$
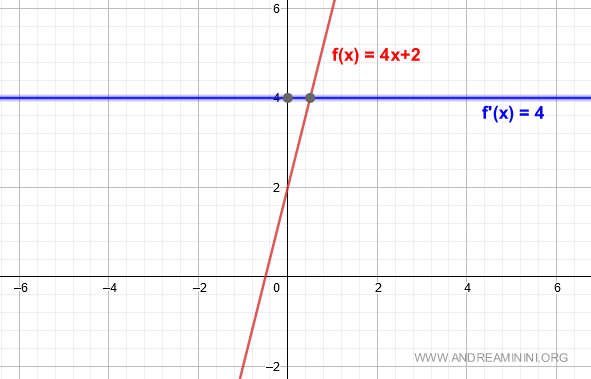
Pertanto
$$ f'(x)=4 $$
La derivata prima della funzione f(x) è la costante k ossia il coefficiente m della funzione lineare.
E così via.
