La derivata della funzione seno

La derivata della funzione seno x è coseno x. $$ D[sin x] = cos x $$

La dimostrazione

Per dimostrare e spiegare questa regola di derivazione, parto dalla funzione trigonometrica del seno per x.

$$ f(x) = sin \:\:x $$

Poi calcolo il limite del rapporto incrementale per ottenere la funzione derivata prima

$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $$

dove

$$ f(x) = sin \:\:x $$

$$ f(x+h) = sin \:\: (x+h) $$

Sostituisco le funzioni nel rapporto incrementale

$$ \lim_{h \rightarrow 0} \frac{sin \:\: (x+h)-sin\:\: (x)}{h} $$

Secondo una formula trigonometrica $$ sin \:\: a - sin \:\: b = 2 \cdot sin \:\: \frac{a-b}{2} \cdot cos \:\: \frac{a+b}{2} $$

Quindi posso riscrivere il rapporto incrementale

$$ \lim_{h \rightarrow 0} \frac{ 2 \cdot sin \:\: \frac{(x+h)-(x)}{2} \cdot cos \:\: \frac{(x+h)+(x)}{2} }{h} $$

$$ \lim_{h \rightarrow 0} \frac{ 2 \cdot sin \:\: \frac{h}{2} \cdot cos \:\: (\frac{2x+h}{2}) }{h} $$

$$ \lim_{h \rightarrow 0} \frac{ 2 \cdot sin \:\: \frac{h}{2} \cdot cos \:\: (x + \frac{h}{2}) }{h} $$

Ora moltiplico entrambi i membri del rapporto per 1/2.

$$ \lim_{h \rightarrow 0} \frac{ [ 2 \cdot sin \:\: \frac{h}{2} \cdot cos \:\: (x + \frac{h}{2} ) ] \cdot \frac{1}{2} }{h \cdot \frac{1}{2} } $$

$$ \lim_{h \rightarrow 0} \frac{ sin \:\: \frac{h}{2} \cdot cos \:\: (x + \frac{h}{2}) }{ \frac{h}{2} } $$

Scompongo le due componenti del rapporto

$$ \lim_{h \rightarrow 0} \frac{ sin \:\: \frac{h}{2} }{ \frac{h}{2} } \cdot \lim_{h \rightarrow 0} cos \:\: x + \frac{h}{2} $$

Il primo limite è un limite notevole

$$ \lim_{x \rightarrow 0} \frac{sin \: x}{x} = 1 $$

Quindi, posso riscrivere il limite della funzione in

$$ 1 \cdot \lim_{h \rightarrow 0} cos \:\: x + \frac{h}{2} $$

Il secondo limite è uguale a cos(x).

$$ 1 \cdot cos \: x $$

Pertanto la derivata di sin(x) è

$$ f'(x) = cos \: x $$

Ho così dimostrato la derivata del seno.

La rappresentazione grafica

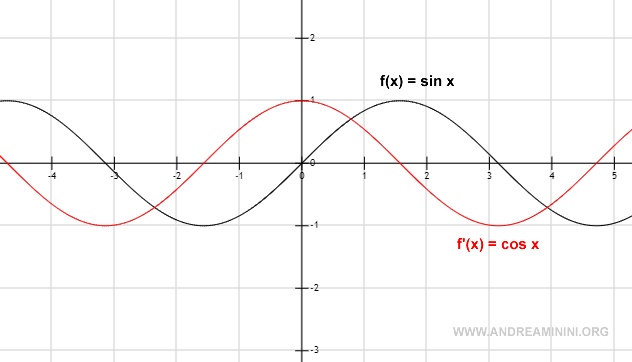
Un esempio pratico

Prendo come esempio la seguente funzione

$$ f(x) = sin \: (x^2)$$

Attenzione. Quando la funzione seno non è semplice, non va applicata soltanto la regola di derivazione elementare perché si tratta di una funzione composta del tipo f(g(x)). Quindi il risultato della precedente funzione non è semplicemente cos(x²).

Si tratta di una funzione composta e devo applicare la regola

$$ f'(x) = f'(g(x)) \cdot g'(x) $$

dove

$$ f'(g(x)) = D[sin(g(x))] = cos(x^2) $$

$$ g'(x) = D[x^2] = 2x $$

Quindi, sostituendo i valori la derivata della funzione composta diventa

$$ f'(x) = f'(h(x)) \cdot g'(x) $$

$$ f'(x) = cos(x^2) \cdot 2x $$

In conclusione la derivata della funzione sin x² è

$$ f'(x) = 2x \cdot cos(x^2) $$

La rappresentazione grafica

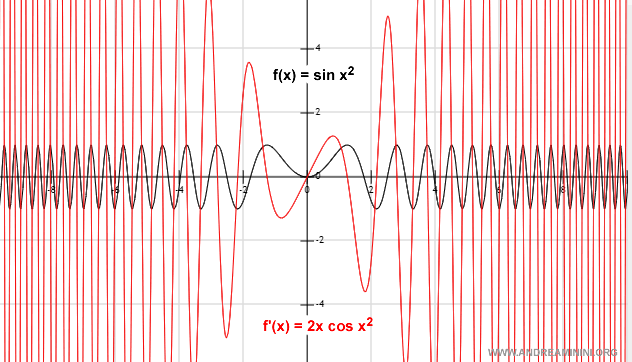
E così via.