Il calcolo differenziale
Cos'è il calcolo differenziale
Secondo una definizione del calcolo differenziale in analisi matematica
Il calcolo differenziale studia le variazioni infinitesimali di una funzione. Una delle principali operazioni è la derivazione.
Questa definizione è molto sintetica, forse troppo, e non rende chiara l'idea a chi si avvicina per la prima volta a questo concetto.
Per spiegarlo faccio un esempio pratico.
Un esempio pratico
Un punto P si muove in una funzione f(t).
Lo spazio percorso dal punto P a partire da un'origine è in funzione del tempo (t).
$$ s=f(t) $$
Nota. In modo equivalente potrei dire che la posizione del punto P sulla retta è in funzione del tempo. Sarebbe però più difficile da capire.
Disegno un diagramma cartesiano ponendo lo spazio s sulle ordinate e il tempo sulle ascisse.
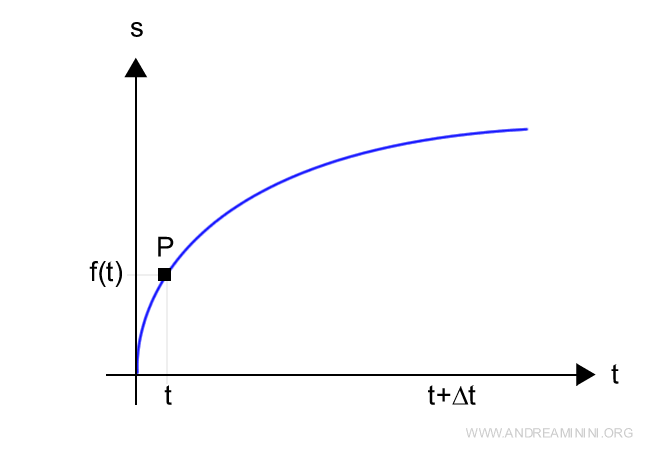
Dopo un lasso di tempo Δt, lo spazio percorso (s') è il seguente:
$$ s'=f(t+Δt) $$
Aggiungo il punto P' sul diagramma cartesiano
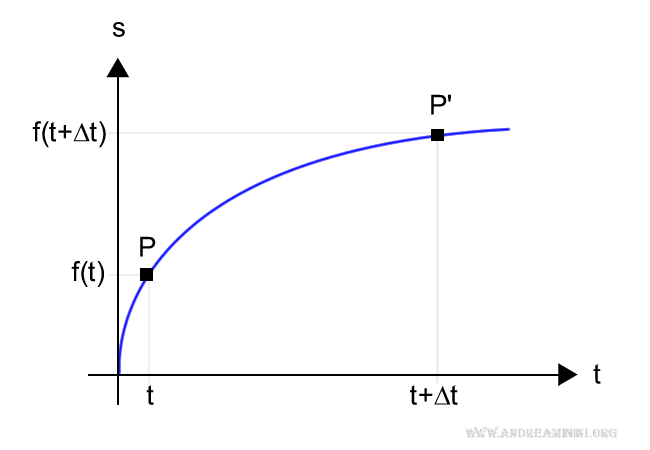
Quindi, per conoscere lo spazio percorso in due istanti diversi t e t+Δt, dovrei calcolare
$$ s'-s = f(t+Δt)-f(t) $$
Sul diagramma cartesiano
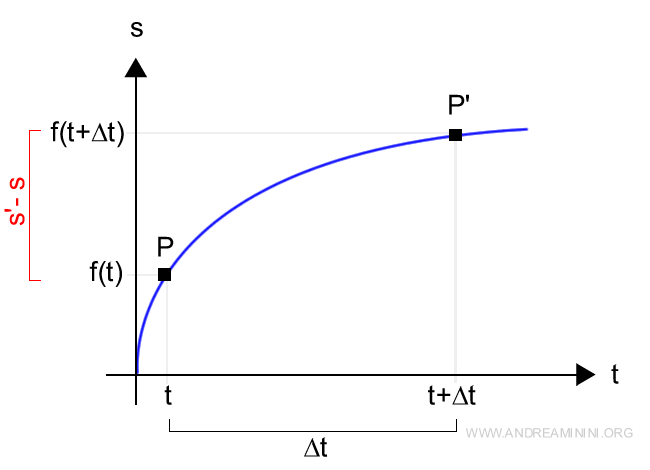
Per conoscere la velocità media dello spostamento
$$ \frac{f(t+Δt)-f(t)}{Δt} $$
Quest'ultimo rapporto è detto rapporto incrementale della variabile.
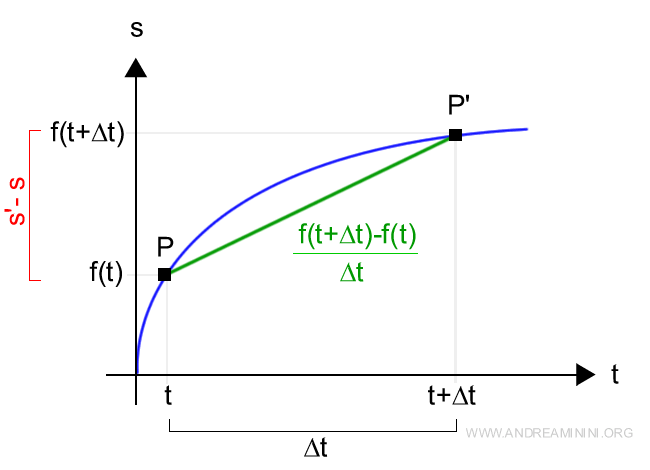
Se però volessi conoscere la velocità del punto in un particolare istante, ad esempio nel punto P, la velocità media non mi sarebbe d'aiuto perché la velocità non è costante nel tempo. Inizialmente è più veloce, poi rallenta.
Come si calcola la velocità istantanea?
Per calcolare la velocità istantanea nell'istante t, ossia v(t), basta fare il limite del rapporto incrementale per Δt tendente a zero
$$ v(t)= \lim_{Δt \rightarrow 0} \frac{f(t+Δt)-f(t)}{Δt} $$
Questa funzione mi permette di calcolare la velocità del punto P nell'istante t.
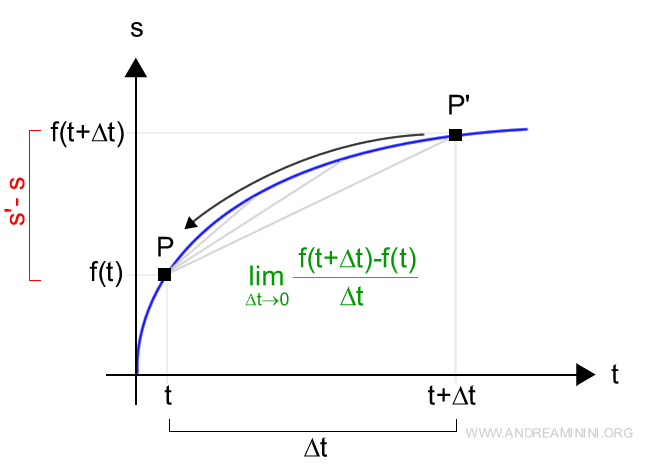
Il limite del rapporto incrementale mi permette di trovare la velocità istantanea nell'istante t.
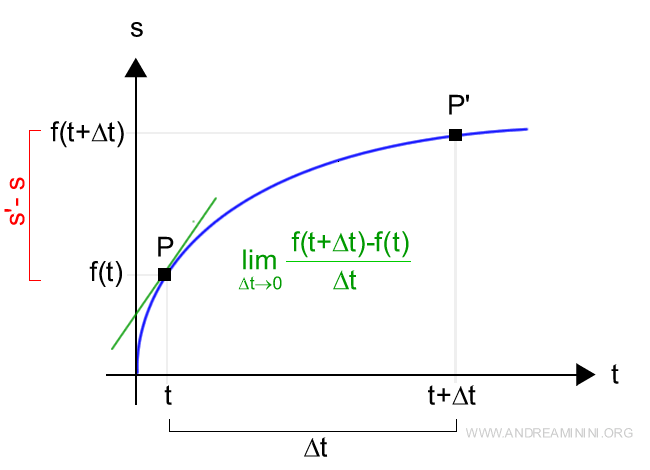
La velocità istantanea coincide con la retta tangente nel punto P.
Il limite del rapporto incrementale è detta operazione di derivazione.
A cosa serve il calcolo differenziale?
Il calcolo differenziale mi permette di studiare il comportamento della funzione in ogni suo punto.
Se è crescente o decrescente, se è una curva concava o convessa, se c'è un asintoto, ecc.
E così via.
