La derivata della radice quadrata
La derivata di una radice quadrata è $$ D[\sqrt{x}] = \frac{1}{2 \cdot \sqrt{x}} $$
La dimostrazione
Per dimostrare questa semplice regola di derivazione, prendo come esempio la funzione
$$ f(x) = \sqrt{x} $$
Il limite del rapporto incrementale della funzione è
$$ \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $$
Dove
$$ f(x)=\sqrt{x} $$
$$ f(x+h)=\sqrt{x+h} $$
Sostituisco le funzioni f(x) e f(x+h) nel rapporto incrementale
$$ \lim_{h \rightarrow 0} \frac{\sqrt{x+h}-\sqrt{x}}{h} $$
Per semplificare il rapporto incrementale, moltiplico il numeratore e il denominatore
$$ \lim_{h \rightarrow 0} \frac{\sqrt{x+h}-\sqrt{x}}{h} \cdot \frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}} $$
Poi svolgo i calcoli algebrici al numeratore
$$ \lim_{h \rightarrow 0} \frac{\sqrt{x+h}\cdot (\sqrt{x+h}+\sqrt{x} ) -\sqrt{x} \cdot (\sqrt{x+h}+\sqrt{x})}{h \cdot \sqrt{x+h}+\sqrt{x} } $$
$$ \lim_{h \rightarrow 0} \frac{ \sqrt{x+h} \cdot \sqrt{x+h} + \sqrt{x+h} \cdot \sqrt{x} -\sqrt{x} \cdot \sqrt{x+h} - \sqrt{x} \sqrt{x})}{h \cdot \sqrt{x+h}+\sqrt{x} } $$
$$ \lim_{h \rightarrow 0} \frac{(x+h) + \sqrt{x^2+hx} - \sqrt{x^2+hx} -x}{h \cdot \sqrt{x+h}+\sqrt{x} } $$
$$ \lim_{h \rightarrow 0} \frac{h}{h \cdot \sqrt{x+h}+\sqrt{x} } $$
$$ \lim_{h \rightarrow 0} \frac{1}{ \sqrt{x+h}+\sqrt{x} } $$
Il limite per h tendente a zero è
$$ \lim_{h \rightarrow 0} \frac{1}{ \sqrt{x+h}+\sqrt{x} } = \frac{1}{ \sqrt{x}+\sqrt{x} } = \frac{1}{ 2\sqrt{x} } $$
Ho così dimostrato la derivata della radice quadrata √x
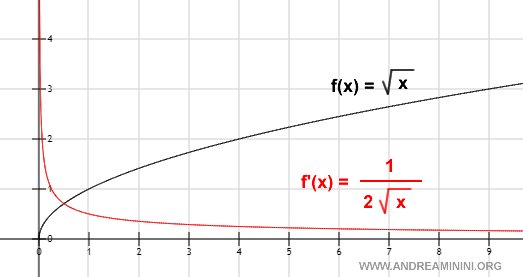
Rappresentazione grafica
Un esercizio svolto ( esempio )
Devo calcolare la derivata di questa funzione
$$ f(x) = \sqrt{3x+1} $$
Attenzione. All'atto pratico bisogna fare molta attenzione quando si calcola la derivata di una radice, perché spesso non si tratta di una semplice derivata di una radice. Ad esempio, in questo caso la derivata NON è $$ \frac{1}{2 \sqrt{3x+1}} \:\:\: errore $$ $$ \frac{1}{2 \sqrt{3}} \:\:\: errore $$
In questo caso si tratta di una funzione composta g[h(x)] dove
$$ g(x) = \sqrt{h(x)} $$
$$ h(x) = 3x+1 $$
Quindi, va usata la regola di derivazione delle funzioni composte.
La regola di derivazione di una funzione composta è la seguente:
$$ g'[h(x)] \cdot h'(x) $$
Dove
$$ g'[h(x)] = D[ \sqrt{h(x)} ] = \frac{1}{2\sqrt{h(x)}} = \frac{1}{2\sqrt{3x+1}} $$
$$ h'(x) = D[3x+1] = 3 $$
Quindi
$$ g'[h(x)] \cdot h'(x) = \frac{1}{2\sqrt{3x+1}} \cdot 3 = \frac{3}{2\sqrt{3x+1}} $$
La derivata prima di f(x) è
$$ f'(x) = \frac{3}{2\sqrt{3x+1}} $$
E così via
