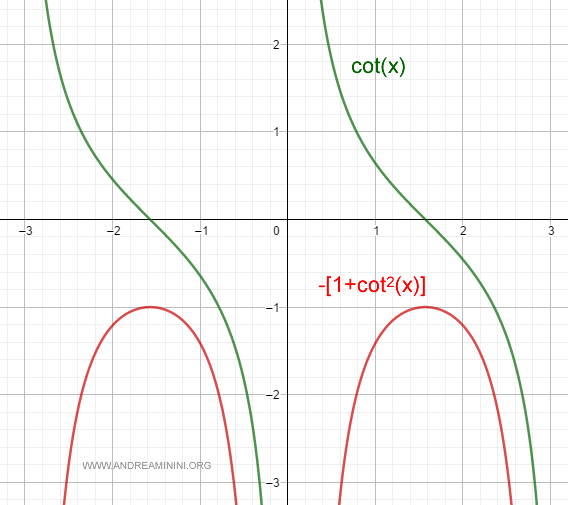
La derivata della cotangente

La derivata della funzione cotangente è $$ D[cot \: x] = \frac{ - 1 }{ [sin \:x]^2 } = - (1 + cot^2 \: x ) $$

Dimostrazione

Per spiegare la derivata della cotangente utilizzo una regola di equivalenza della trigonometria, secondo la quale la cotangente è uguale al rapporto tra coseno e seno.

$$ cot \:x = \frac{cos \:x}{ sin \:x} $$

Nota. La spiegazione è molto simile alla derivata di una tangente.

Pertanto, la derivata della tangente è uguale alla derivata del rapporto tra coseno e seno.

$$ D[cot \:x ]= D[ \frac{cos \:x}{ sin \:x}] $$

Ora diventa tutto molto più semplice perché conosco già le derivate del seno e del coseno.

$$ D[sin \: x] = cos \: x $$

$$ D[cos \: x] = -sin \: x $$

Applico la regola di derivazione del rapporto di due funzioni

$$ D[cot \:x ]= D[ \frac{cos \:x}{ sin \:x}] $$

$$ \frac{D[cos \:x] \cdot sin \: x - cos \:x \cdot D[sin \:x]}{ [sin \:x]^2 } $$

$$ \frac{-sin \:x \cdot sin \: x - cos \:x \cdot cos \:x}{ [sin \:x]^2 } $$

$$ \frac{ -sin^2 \:x - cos^2 \:x }{ [sin \:x]^2 } $$

$$ \frac{ - ( sin^2 \:x + cos^2 \:x ) }{ [sin \:x]^2 } $$

Secondo una regola della trigonometria, la somma dei quadrati del seno e del coseno è uguale a uno. $$ sin^2 \:x + cos^2 \: x = 1 $$

Quindi posso scrivere il risultato anche in questa forma:

$$ \frac{ - ( sin^2 \:x + cos^2 \:x ) }{ [sin \:x]^2 } $$

$$ \frac{ - 1 }{ [sin \:x]^2 } $$

Secondo una regola di equivalenza trigonometrica tra seno e cotangente $$ sin \: x = \frac{1}{\sqrt(1+cot^2 \:x)} $$

A questo punto sostituisco i termini e ottengo

$$ \frac{-1}{sin^2 \:x} = \frac{-1}{ \begin{pmatrix} \frac{1}{\sqrt(1+cot^2 \:x)} \end{pmatrix}^2 } = \frac{-1}{ \frac{1}{(1+cot^2 \:x)} } = -1 \cdot (1+cot^2 \:x) = -(1+cot^2 \:x)$$

Ho così dimostrato la formula della derivata della cotangente.