Massimo e minimo con le derivate
Il massimo e il minimo di una funzione f(x) può essere studiato con le derivate.
- Se la derivata prima è nulla in x0 $$ f'(x_0) = 0 $$ allora la funzione ha
- un massimo locale se la derivata seconda è negativa $$ f"(x_0) < 0 $$
- un minimo locale se la derivata seconda è positiva $$ f"(x_0) > 0 $$
Il criterio generale
Il criterio per riconoscere un punto di minimo e massimo si può generalizzare in questo modo
Se la derivata di ordine k è nulla in x0 e k è dispari.
$$ f^{k}(x_0) = 0 \:\:\:\: con \:\:\: k=dispari$$
Allora la funzione ha
- un massimo locale se la derivata di ordine k+1 è negativa $$ f^{k+1}(x_0) < 0 $$
- un minimo locale se la derivata di ordine k+1 è positiva $$ f^{k+1}(x_0) > 0 $$
- né un massimo, né un minimo se la derivata di ordine k+1 è nulla e quella di ordine k+2 è diversa da zero $$ f^{k+1}(x_0) = 0 \:\: ∧ \:\: f^{k+2}(x_0) \ne 0 $$ In questo caso la funzione ha un flesso.
Nota. Se la derivata di ordine k è nulla e k è pari, allora la funzione non ha né un minimo né un massmo in x0 se la derivata k+1 è diversa da zero. In questi punti la funzione ha un flesso.

Dimostrazione
Per dimostrare questo criterio parto dalla formula di Taylor con una funzione continua e derivabile n volte in x0.
$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x-x_0)^k + R_n(x) $$
ossia
$$ f(x) = f(x_0) + f^{(1)}(x_0) \cdot \frac{ (x-x_0)^1 }{1!} + f^{(2)}(x_0) \cdot \frac{ (x-x_0)^2 }{2!} + ... + f^{(n)}(x_0) \cdot \frac{ (x-x_0)^n }{n!} + R_n $$
Considero nulle le derivate della funzione fino all'ordine n-1
$$ f'(x_0) = f"(x_0) = f^{(3)}(x_0) = ... = f^{(n-1)}(x_0) = 0 $$
Quindi la formula di Taylor si riduce a
$$ f(x) = f(x_0) + f^{(n)}(x_0) \cdot \frac{ (x-x_0)^n }{n!} + R_n $$
Per ipotesi considero la derivata di ordine n positiva in x0.
Quindi si tratta di un minimo.
$$ f^{(n)}(x_0) > 0 $$
Nota. La dimostrazione è comunque la stessa se considerassi la derivata f(n) negativa in x0. Salvo per il fatto che si tratterebbe di un massimo locale anziché di un minimo.
Calcolo il limite
$$ \lim_{x \rightarrow x_0} \frac{f(x)-f(x_0)}{(x-x_0)^n} $$
$$ \lim_{x \rightarrow x_0} \frac{[ f(x_0) + f^{(n)}(x_0) \cdot \frac{ (x-x_0)^n }{n!} + R_n ]-f(x_0)}{(x-x_0)^n} $$
$$ \lim_{x \rightarrow x_0} \frac{ f^{(n)}(x_0) \cdot \frac{ (x-x_0)^n }{n!} + R_n }{(x-x_0)^n} $$
$$ \lim_{x \rightarrow x_0} [ f^{(n)}(x_0) \cdot \frac{ (x-x_0)^n }{n!} + R_n ] \cdot \frac{1}{(x-x_0)^n} $$
$$ \lim_{x \rightarrow x_0} \frac{ f^{(n)}(x_0) }{n!} + \frac{R_n}{(x-x_0)^n} = \frac{ f^{(n)}(x_0) }{n!} > 0 $$
Pertanto, il limite iniziale è maggiore di zero.
$$ \lim_{x \rightarrow x_0} \frac{f(x)-f(x_0)}{(x-x_0)^n} > 0 $$
A questo punto posso analizzare le due situazioni in cui n è pari o dispari
- se n è pari il denominatore (x-x0)n è sempre positivo, quindi f(x)>f(x0) in ogni punto dell'intorno (x0-δ,x0+δ). Quindi x0 è un minimo locale.
- se n è dispari il denominatore (x-x0)n cambia segno nell'intorno destro e sinistro di x0. Quindi x0 non può essere un minimo locale.
In conclusione, il punto x0 è un minimo soltanto se la derivata f(n)≠0 è di ordine pari.
Un esempio pratico
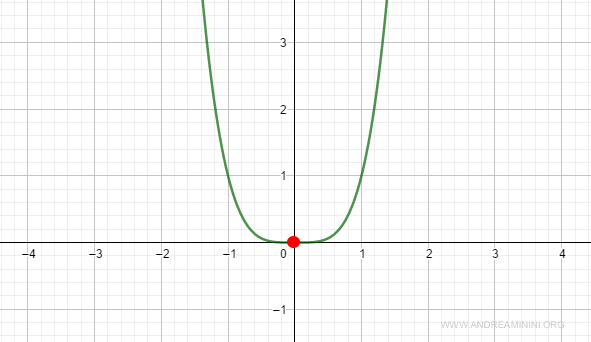
Esempio 1 ( n = pari )
Ho la funzione
$$ f(x) = x^4 $$
Nel punto x0=0 le derivate di ordine uno, due e tre sono nulle
$$ f^{1}(x0) = 4x^3 = 4(0)^3 = 0 $$
$$ f^{2}(x0) = 12x^2 = 12(0)^2 = 0 $$
$$ f^{3}(x0) = 24x = 24(0) = 0 $$
La derivata di ordine n=4 (pari) è positiva in x0
$$ f^{4}(x0) = 24 > 0 $$
Pertanto, nel punto x0 la funzione ha un minimo.
Esempio 2 ( n = dispari )
Ho la funzione
$$ f(x) = x^3 $$
Nel punto x=e la derivata prima e seconda sono nulle
$$ f^{1}(x0) = 3x^2 = 3(0)^2 = 0 $$
$$ f^{2}(x0) = 6x = 6(0) = 0 $$
La derivata terza n=3 (dispari) è invece positiva
$$ f^{3}(x0) = 6 > 0 $$
In questo caso è ben evidente che non si tratta di un minimo.
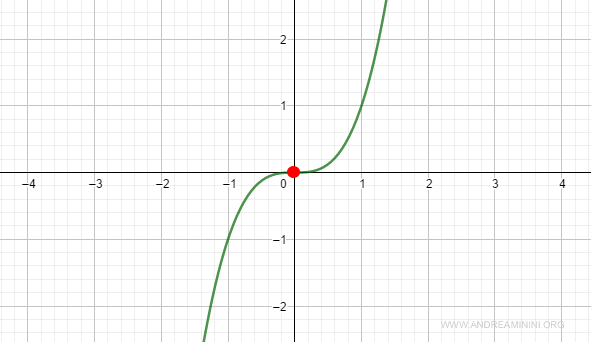
Nel punto x0 c'è un flesso.
E così via.
