La relazione tra il lato e l'altezza del triangolo equilatero
La lunghezza di un lato del triangolo equilatero si può calcolare conoscendo l'altezza tramite la seguente formula $$ l = \frac{2h}{ \sqrt{3} } $$
A volte la stessa formula viene presentata in questa forma equivalente:
$$ l = \frac{2 \cdot \sqrt{3} }{3} h $$
Il risultato è sempre lo stesso.
La formula inversa consiste nel calcolare l'altezza (h) del triangolo equilatero conoscendo il lato (l) $$ h = \frac{ \sqrt{3} }{2} l $$
Un esempio pratico
Prendo come esempio un triangolo equilatero di cui conosco la lunghezza dei lati (3) e dell'altezza h=2.5981
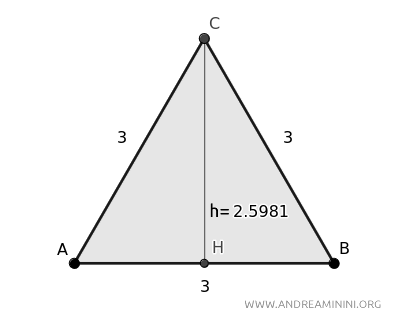
Applico la formula per verificare se la relazione tra il lato e l'altezza del triangolo equilatero è corretta.
$$ l = \frac{2h}{ \sqrt{3} } $$
Sostituisco l'altezza h=2.5981 e svolgo i calcoli per ottenere la lunghezza del lato.
$$ l = \frac{2 \cdot 2.5981}{ \sqrt{3} } $$
$$ l = \frac{5.1962}{ \sqrt{3} } $$
$$ l = 3 $$
Il risultato è la lunghezza (3) del lato del triangolo equilatero.
La dimostrazione
Considero un triangolo equilatero.
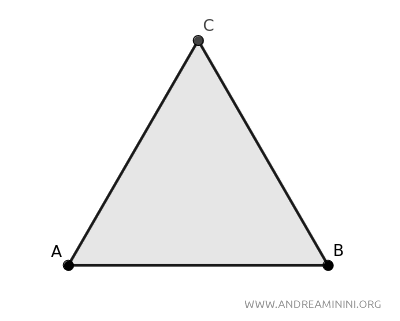
Per definizione tutti i lati hanno la stessa lunghezza l
$$ l = \overline{AB} = \overline{BC} = \overline{AC} $$
Traccio l'altezza (h) del triangolo rispetto alla base AB.
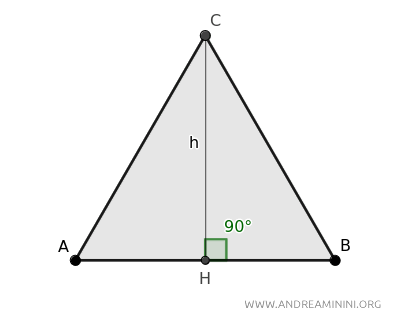
In un triangolo equilatero, l'altezza interseca perpendicolarmente il punto medio H della base (AB).
Quindi, l'altezza suddivide il triangolo equilatero in due triangoli rettangoli congruenti.
A questo punto, utilizzo il teorema di Pitagora per calcolare il cateto HC del triangolo rettangolo AHC.
$$ \overline{HC} = \sqrt{\overline{AC}^2 - \overline{AH}^2} $$
Indico il segmento HC come l'altezza h e il segmento AC come il lato l del triangolo equilatero ABC.
$$ h = \sqrt{l^2 - \overline{AH}^2} $$
Il segmento AH è la metà della base del triangolo equilatero ABC, ovvero del lato AB=l, quindi posso scrivere AH come l/2
$$ h = \sqrt{l^2 - ( \frac{l}{2} )^2} $$
Svolgo i calcoli algebrici
$$ h = \sqrt{l^2 - \frac{l^2}{2^2} } $$
$$ h = \sqrt{l^2 - \frac{l^2}{4} } $$
$$ h = \sqrt{\frac{4l^2 - l^2}{4} } $$
$$ h = \sqrt{\frac{3l^2}{4} } $$
$$ h = \frac{l}{2} \sqrt{3} $$
Ho così ottenuto la formula che calcola l'altezza conoscendo il lato del triangolo equilatero.
Moltiplico entrambi i membri dell'equazione per 2/√3 per ricavare il lato (l)
$$ h \cdot \frac{2}{\sqrt{3}} = \frac{l}{2} \sqrt{3} \cdot \frac{2}{\sqrt{3}} $$
$$ \frac{2}{\sqrt{3}} h = l $$
In questo modo ottengo la formula inversa che calcola il lato conoscendo l'altezza del triangolo equilatero.
$$ l = \frac{2}{\sqrt{3}} h $$
Nota. Talvolta quest'ultima formula viene presentata anche in questa forma alternativa con il radicale al numeratore. Moltiplico e divido il secondo membro dell'equazione per la radice quadrata di 3. $$ l = \frac{2}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} \cdot h $$ $$ l = \frac{2 \cdot \sqrt{3} }{\sqrt{3} \cdot \sqrt{3}} h $$ $$ l = \frac{2 \cdot \sqrt{3} }{3} h $$
E così via.
