Relazione tra lato del triangolo equilatero e raggio del cerchio circoscritto
Il lato di un triangolo equilatero è uguale al raggio del cerchio circoscritto per la radice quadrata di tre. $$ l = r \cdot \sqrt{3} $$
Un esempio pratico
Considero il triangolo equilatero ABC e una circonferenza circoscritta con centro O e raggio r.
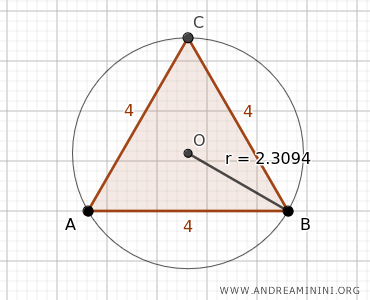
In questo caso il raggio del cerchio circoscritto al triangolo è r=2.3094.
Applico la formula per calcolare il lato del triangolo equilatero.
$$ l = r \cdot \sqrt{3} $$
$$ l = 2.3094 \cdot \sqrt{3} = 4 $$
Il risultato è la lunghezza del lato del triangolo equilatero.
La dimostrazione
Per dimostrare questa formula considero un esagono regolare e un cerchio circoscritto con centro O e raggio r.
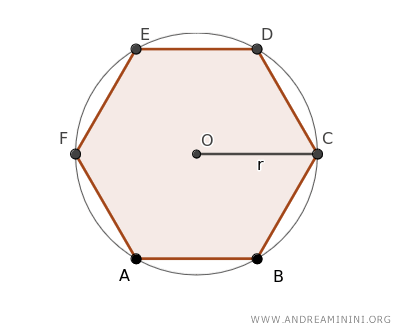
Scelgo tre vertici non adiacenti dell'esagono ( ad esempio A, E, C ) e li collego tra loro, ottenendo un triangolo al centro AEC e tre triangoli ai margini (ABC, AEF, CDE).
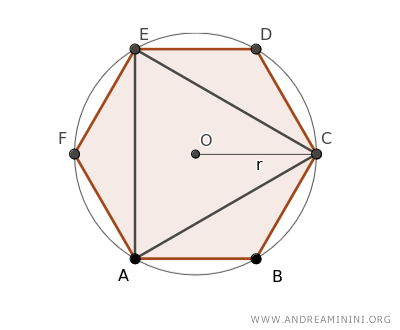
I triangoli ai margini sono congruenti per il primo teorema di congruenza dei triangoli, perché hanno i lati obliqui uguali ai lati dell'esagono e l'angolo tra di essi congruente (120)°.
Pertanto hanno tutti i lati congruenti.
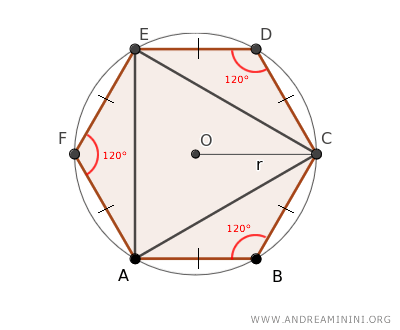
Nota. Un esagono regolare ha tutti i lati congruenti e gli angoli congruenti a 120°.
Quindi, il triangolo al centro AEC è un triangolo equilatero.
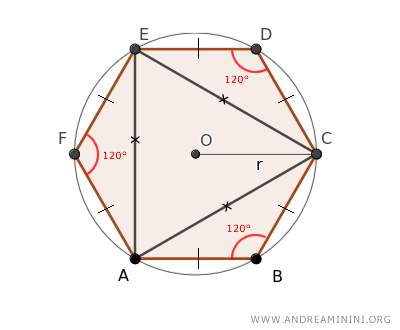
A questo punto cerco di calcolare la misura di un lato qualsiasi del triangolo equilatero.
Per farlo traccio il segmento CF che coincide con il diametro del cerchio d=2r ossia con il doppio del raggio.
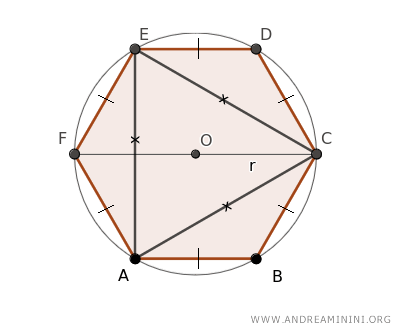
Osservando la figura si forma un altro triangolo ECF che ha in comune il lato EC con il triangolo equilatero AEC-
L'angolo sul vertice E del triangolel ECF è un angolo retto perché è un angolo alla circonferenza che insiste su una semicirconferenza.
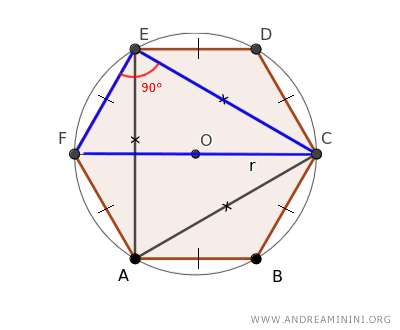
Questo vuol dire che il triangolo ECF è un triangolo rettangolo e posso applicare il teorema di Pitagora per calcolare la lunghezza del lato EC
$$ \overline{EC} = \sqrt{ \overline{FC}^2 - \overline{EF}^2 } $$
Dove il segmento FC è il diametro d=2r della circonferenza circoscritta.
$$ \overline{EC} = \sqrt{ (2r)^2 - \overline{EF}^2 } $$
Il segmento EF è un lato dell'esagono regolare.
Sapendo che il lato di un esagono regolare è congruente con il raggio della circonferenza circoscritta, sostituisco EF=r
$$ \overline{EC} = \sqrt{ (2r)^2 - r^2 } $$
Svolgo i calcoli algebrici e semplifico
$$ \overline{EC} = \sqrt{ 4r^2 - r^2 } $$
$$ \overline{EC} = \sqrt{ 3r^2 } $$
$$ \overline{EC} = r \sqrt{ 3 } $$
Il segmento EC è un lato del triangolo equilatero AEC ed è congruente agli altri lati del triangolo.
Questo dimostra che il lato di un triangolo equilatero è uguale al raggio del cerchio circoscritto per la radice quadrata di tre.
E così via.
