Relazione tra lato e raggio del cerchio inscritto in un triangolo equilatero
La relazione tra il lato del triangolo equilatero e il raggio del cerchio inscritto $$ l = 2r \sqrt{3} $$
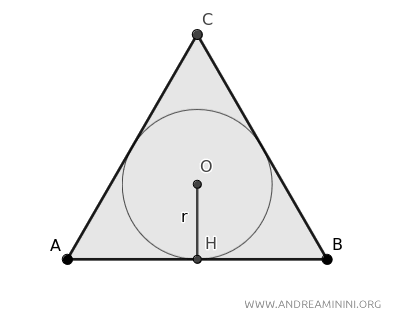
Un esempio pratico
Prendo come esempio un triangolo equilatero con i lati di lunghezza pari a 3 e un cerchio inscritto di raggio r=0.866
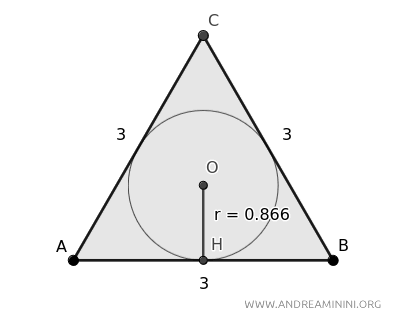
La formula che lega il raggio del cerchio inscritto al lato del triangolo equilatero è la seguente:
$$ l = 2r \sqrt{3} $$
In questo caso il raggio è r=0.866
$$ l = 2 \cdot 0.866 \cdot \sqrt{3} $$
$$ l = 1.7321 \cdot \sqrt{3} $$
$$ l = 3 $$
Il risultato è la lunghezza del lato del triangolo equilatero.
La dimostrazione
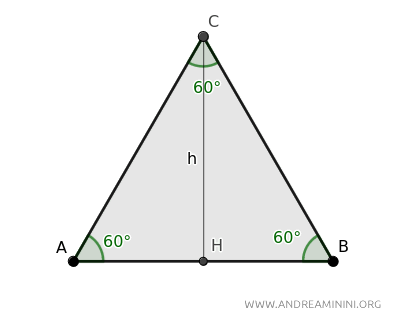
Considero un triangolo equilatero ABC.
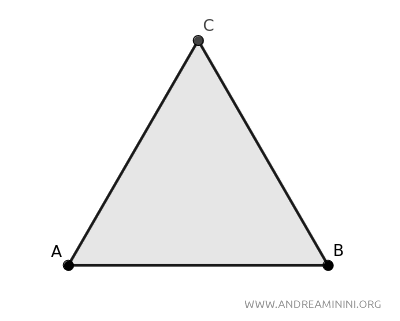
Traccio l'altezza h=CH del triangolo equilatero rispetto al lato AB scelto come base.
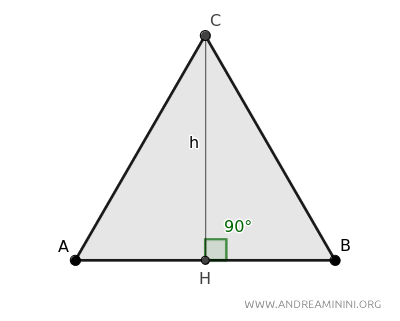
Nel triangolo equilatero l'altezza cade perpendicolarmente nel punto medio H della base AB, dividendola in due parti congruenti AH=BH.
Inoltre, l'altezza è anche la mediana dell'angolo interno opposto alla base.
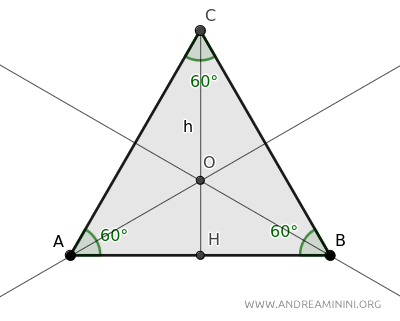
A questo punto traccio le altre due mediane degli angoli adiacenti alla base.
Le due mediane si intersecano nel baricentro O del triangolo.
Disegno il cerchio inscritto nel triangolo equilatero, ovvero l'incerchio, che tocca i lati del triangolo in tre punti di tangenza.
Il segmento OH è il raggio del cerchio inscritto (incerchio).
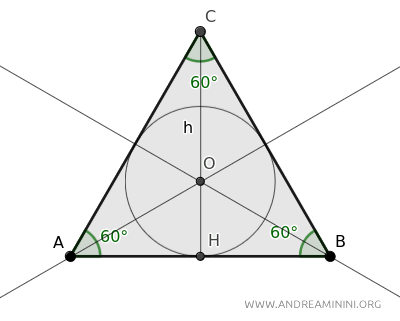
Sapendo che in un triangolo il baricentro divide il segmento della mediana in un rapporto pari a 2:1, ossia in due parti pari a 1/3 e 2/3, deduco che il raggio r=OH è uguale a 1/3 dell'altezza CH.
$$ \overline{OH} = \frac{1}{3} \cdot \overline{CH} $$
Pertanto, il segmento CH è tre volte il segmento OH
$$ \overline{CH} = 3 \cdot \overline{OH} $$
Dove OH=r è il raggio del cerchio inscritto e CH=h è l'altezza del triangolo equilatero.
$$ h = 3 \cdot r $$
A questo punto basta ricordarsi della relazione tra la lunghezza del lato e l'altezza h in un triangolo equilatero.
$$ h = \frac{l}{2} \sqrt{3} $$
Sostituisco h=3r
$$ 3r = \frac{l}{2} \sqrt{3} $$
Da quest'ultima equazione ricavo il raggio del cerchio inscritto conoscendo la lunghezza del lato.
$$ r = \frac{l}{2 \cdot 3} \sqrt{3} $$
$$ r = \frac{l}{6} \sqrt{3} $$
Moltiplico e divido il secondo membro dell'equazione per la radice quadrata di tre
$$ r = \frac{l}{6} \sqrt{3} \cdot \frac{\sqrt{3}}{\sqrt{3}} $$
$$ r = \frac{l}{6 \sqrt{3} } \cdot ( \sqrt{3} \cdot \sqrt{3} ) $$
$$ r = \frac{l}{6 \sqrt{3} } \cdot 3 $$
$$ r = \frac{l}{2 \sqrt{3} } $$
Infine, calcolo la formula inversa, ossia la lunghezza del lato conoscendo il raggio del cerchio inscritto.
$$ l = 2r \sqrt{3} $$
Questo dimostra la relazione tra il raggio del cerchio inscritto e il lato del triangolo equilatero.
E così via.
