Proporzioni
Una proporzione è un'uguaglianza tra due rapporti x:y=z:w. Si legge "x sta a y come z sta a w".
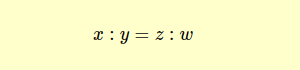
I termini della proporzione x e z sono detti termini antecedenti mentre y e w sono detti conseguenti.
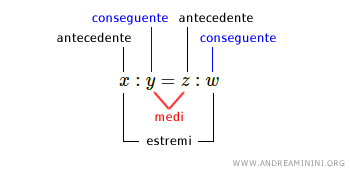
I termini esterni x e w della proporzione sono invece detti estremi, quelli centrali y e z sono detti medi.
In alternativa alla definizione iniziale posso anche affermare che
Una proporzione è un uguaglianza tra due frazioni equivalenti $$ x:y = z:w \Longleftrightarrow \frac{x}{y} = \frac{z}{w} $$
In una proporzione i rapporti x:y e z:y sono frazioni equivalenti
Quindi, posso scrivere la proporzione x:y=z:w anche in questa forma
$$ \frac{x}{y} = \frac{z}{w} $$
Un esempio pratico
Ecco un esempio di proporzione: due sta a quattro come cinque sta a dieci
$$ 2:4 = 5:10 $$
Per verificarla riscrivo la proporzione come uguaglianza tra frazioni equivalenti
$$ \frac{2}{4} = \frac{5}{10} $$
Sono effettivamente due frazioni equivalenti perché il loro prodotto incrociato è uguale
$$ 2 \cdot 10 = 5 \cdot 4 $$
$$ 20 = 20 $$
Pertanto, si tratta di una proporzione
Esempio 2
Considero un altra proporzione: tre sta a nove come cinque sta a quindici
$$ 3:9 = 5:15 $$
Anche questa è una proporzione perché si tratta di un'uguaglianza tra frazioni equivalenti
$$ \frac{3}{9} = \frac{5}{15} $$
Basta semplificare le due frazioni per accorgersi che restituiscono lo stesso risultato
$$ \frac{3:3}{9:3} = \frac{5:5}{15:5} $$
$$ \frac{1}{3} = \frac{1}{3} $$
Esempio 3
Questa uguaglianza invece NON è una proporzione
$$ 4:7 = 6:10 $$
perché le due frazioni non sono frazioni equivalenti
$$ \frac{4}{7} = \frac{6}{10} $$
in quanto il prodotto incrociato delle due frazioni restituisce due risultati diversi
$$ 4 \cdot 10 = 6 \cdot 7 $$
$$ 40 = 42 $$
Pertanto, le due frazioni non sono frazioni equivalenti e l'uguaglianza 4:7 = 6:10 non è una proporzione.
Le proporzioni continue
Una proporzione è detta proporzione continua se i medi o gli estremi sono uguali. $$ x:\color{red}y = \color{red}y:w $$ $$ \color{red}x:y = z:\color{red}x $$
Se un termine compare due volte nei medi è detto medio proporzionale.
Se invece un termine compare due volte negli estremi è detto estremo proporzionale.
Esempio 1
Questa proporzione è continua perché i termini medi sono entrambi uguali a tre
$$ 9:\color{red}3 = \color{red}3:1 $$
In questo caso tre è il termine medio proporzionale.
Nota. Per verificare che 9:3=3:1 sia una proporzione mi basta controllare se le due frazioni sono equivalenti $$ \frac{9}{3} = \frac{3}{1} $$ calcolando il loro prodotto incrociato. $$ 9 \cdot 1 = 3 \cdot 3 $$ $$ 9=9 $$ L'identità è confermata. Sono due frazioni equivalenti. Pertanto, 9:3=3:1 è una proporzione.
Esempio 2
Anche questa proporzione è continua perché i termini estremi sono entrambi uguali a otto
$$ \color{red}8:16 = 4:\color{red}8 $$
In questo caso otto è il termine estremo proporzionale.
Nota. Per verificare che 8:16=4:8 sia effettivamente una proporzione, controllo se le due frazioni sono due frazioni equivalenti $$ \frac{8}{16} = \frac{4}{8} $$ tramite il calcolo del loro prodotto incrociato. $$ 8 \cdot 8 = 4 \cdot 16 $$ $$ 64=64 $$ Il risultato è lo stesso, quindi sono due frazioni equivalenti e l'uguaglianza 9:3=3:1 è una proporzione.
Le proprietà delle proporzioni
Le proporzioni hanno le seguenti proprietà
- Proprietà fondamentale delle proporzioni
Il prodotto dei termini medi è uguale al prodotto dei termini estremi $$ x:y = z:w \Longleftrightarrow y \cdot z = x \cdot w $$ - Proprietà del comporre
$$ x:y = z:w \Longleftrightarrow (x+y):x = (z+w):z $$ $$ x:y = z:w \Longleftrightarrow (x+y):y = (z+w):w $$ - Proprietà dello scomporre
$$ x:y = z:w \Longleftrightarrow (x-y):x = (z-w):z $$ $$ x:y = z:w \Longleftrightarrow (x-y):y = (z-w):w $$ - Proprietà del permutare
$$ x:y = z:w \Longleftrightarrow x:z = y:w $$ $$ x:y = z:w \Longleftrightarrow w:y = z:x $$ - Proprietà dell'invertire
$$ x:y = z:w \Longleftrightarrow y:x = w:z $$
E così via.
